What is the meaning of Barlow Twins?

The Barlow Twins method is an approach in self-supervised learning (SSL) that aims to create embeddings invariant to distortions of the input sample. The method is named after neuroscientist H. Barlow, who proposed the redundancy-reduction principle. In the context of Barlow Twins, this principle is applied to measure the cross-correlation matrix between the outputs of two identical networks fed with distorted versions of a sample. The objective is to make this matrix as close to the identity matrix as possible, ensuring that the embeddings of distorted versions of a sample are similar while minimizing redundancy between the components of these vectors.

Are Barlow Twins contrastive?

The Barlow Twins method is not strictly a contrastive learning method. While both approaches aim to learn representations by comparing different views of the same data, Barlow Twins focuses on reducing redundancy between the components of the output vectors of two identical networks. It does this by ensuring the cross-correlation matrix of the outputs remains close to the identity matrix.

What is the difference between VICReg and Barlow Twins?

Both VICReg and Barlow Twins are methods in self-supervised learning, but they have distinct objectives and mechanisms. While Barlow Twins emphasizes reducing redundancy by aligning the cross-correlation matrix of twin network outputs with the identity matrix, VICReg might have different objectives and techniques to achieve its goals. The differences require a detailed comparison of both methods, available in dedicated research papers or comparative studies.

Back to Blogs

Contents

The Barlow Twins Approach
Key Features of Barlow Twins
Performance and Comparisons
Barlow Twins: Key Takeaways

Encord Blog

Barlow Twins: Self-Supervised Learning

September 11, 2023

5 mins

Back to Blogs

Contents

The Barlow Twins Approach
Key Features of Barlow Twins
Performance and Comparisons
Barlow Twins: Key Takeaways

Written by

Alexandre Bonnet

View more posts

Self-supervised learning (SSL) has emerged as a transformative paradigm in machine learning, particularly in computer vision applications. Unlike traditional supervised learning, where labeled data is a prerequisite, SSL leverages unlabeled data, making it a valuable approach when labeled datasets are scarce. The essence of SSL lies in its ability to process data of lower quality without compromising the ultimate outcomes. This approach mirrors how humans learn to classify objects more closely, extracting patterns and correlations from the data autonomously.

However, a significant challenge in SSL is the potential for trivial, constant solutions. A naive SSL method trivially classifies every example as positive in binary classification, leading to a constant and uninformative solution. This challenge underscores the importance of designing robust algorithms, such as the Barlow Twins, that can effectively leverage the power of SSL while avoiding pitfalls like trivial solutions.

In the subsequent sections, we will delve deeper into the Barlow Twins approach to SSL, a new approach developed by Yann LeCun and the team at Facebook. We will also explore its unique features, benefits, and contribution to the ever-evolving landscape of self-supervised learning in machine learning.

The Barlow Twins Approach

The Barlow Twins method, named in homage to neuroscientist H. Barlow's redundancy-reduction principle, presents a novel approach to self-supervised learning (SSL). This method is particularly significant in computer vision, where SSL has rapidly bridged the performance gap with supervised methods.

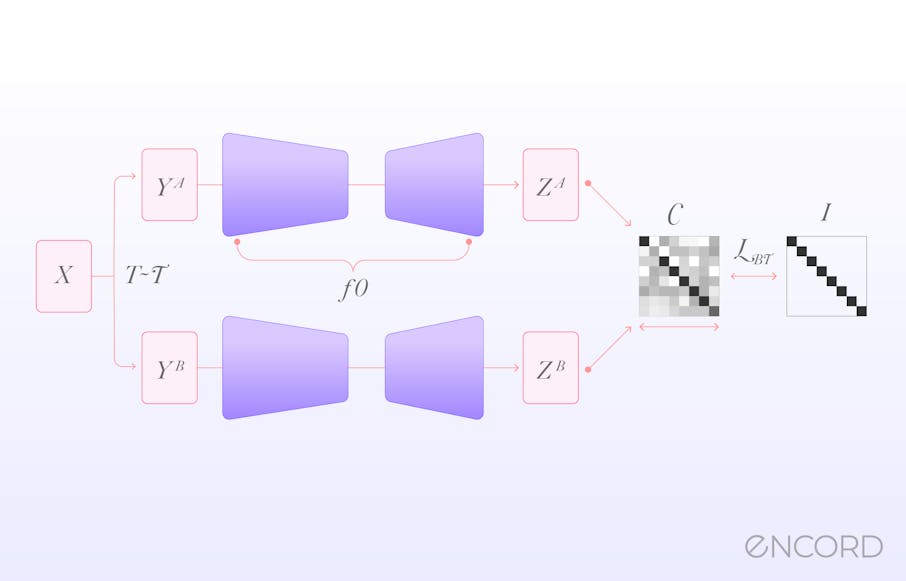
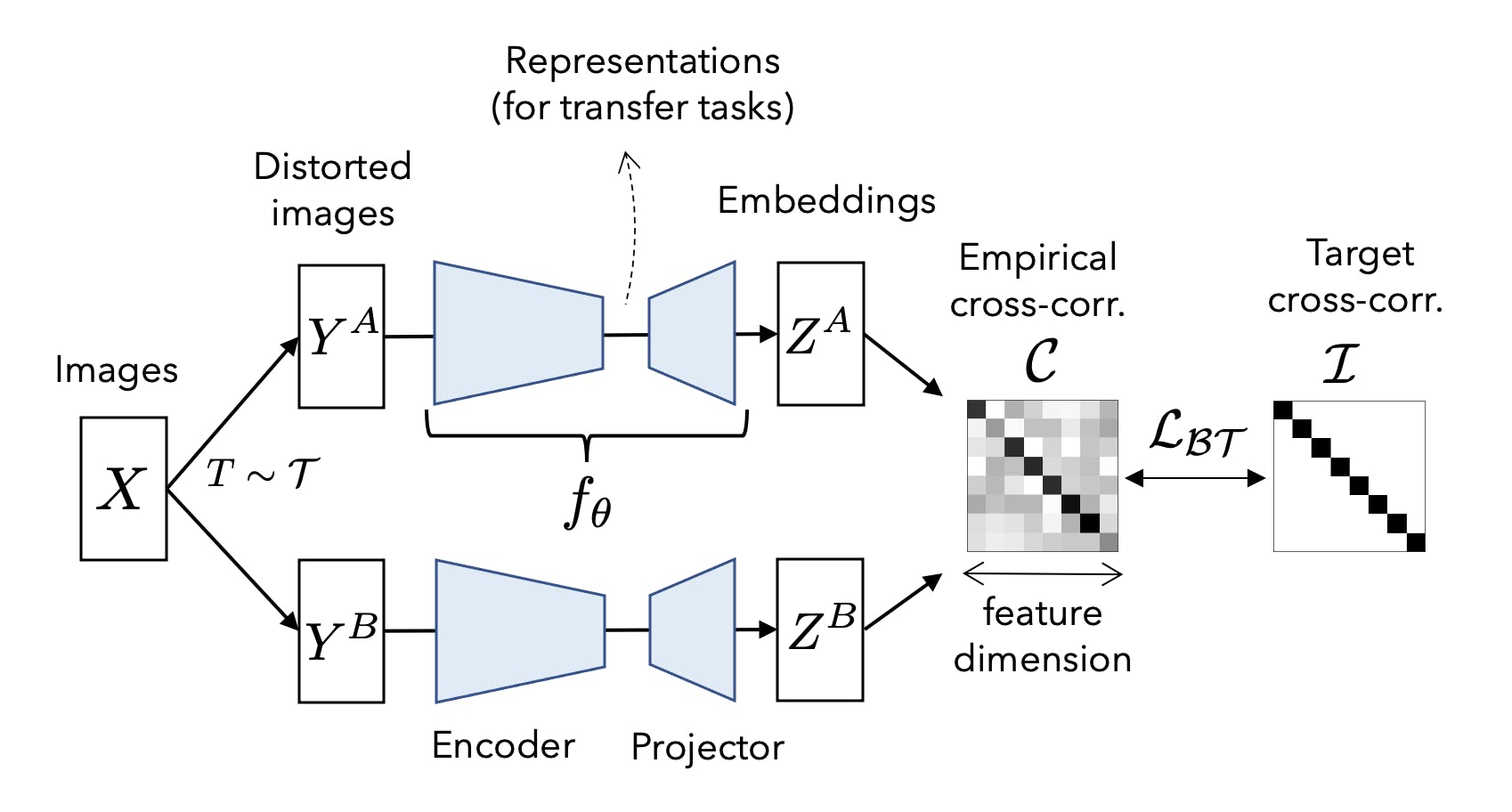
Central to the Barlow Twins approach is its unique objective function, designed to naturally prevent the collapse often observed in other SSL methods. This collapse typically results in trivial, constant solutions, a challenge many SSL algorithms grapple with. The Barlow Twins method addresses this by measuring the cross-correlation matrix between the outputs of two identical neural networks. These networks are fed with distorted versions of a sample, and the objective is to make this matrix as close to the identity matrix as possible.

The role of the cross-correlation matrix is pivotal. By ensuring that the embedding vectors of distorted versions of a sample are similar, the method minimizes redundancy between the components of these vectors. This enhances the quality of the embeddings and ensures that the learned representations are robust and invariant to the applied distortions.

Image Classification with Barlow Twins

Barlow Twin Architecture

Imagine you have many images of cats and dogs, but they must be labeled. You want to train a machine-learning model to distinguish between cats and dogs using this unlabeled dataset.

Here is the Barlow Twins approach:

Data Augmentation: Create two distorted versions for each image in the dataset. For instance, one version might be a cropped section of the original image, and the other might be the same cropped section but with altered brightness or color.
Twin Neural Networks: Use two identical neural networks (the "twins"). Feed one distorted version of the image into the first network and the other distorted version into the second network.
Objective Function: The goal is to make the outputs (embeddings) of the two networks as similar as possible for the same input image, ensuring that the networks recognize the two distorted versions as being of the same class (either cat or dog). At the same time, the Barlow Twins method aims to reduce redundancy in the embeddings. This is achieved by ensuring that the cross-correlation matrix of the embeddings from the two networks is close to an identity matrix. In simpler terms, the method ensures that each embedding component is as independent as possible from the other components.
Training: The twin networks are trained using the above objective. Over time, the networks learn to produce similar embeddings for distorted versions of the same image and different embeddings for images of different classes (cats vs. dogs).
Representation Learning: Once trained, you can use one of the twin networks (or both) to extract meaningful representations (embeddings) from new images. These representations can then be used with a simple linear classifier for various tasks, such as classification.

Barlow Twins Loss Function

The primary objective of the Barlow Twins method is to reduce redundancy in the representations learned by neural networks. To achieve this, the method uses two identical neural networks (often called "twins") that process two distorted versions of the same input sample. The goal is to make the outputs (or embeddings) of these networks as similar as possible for the same input while ensuring that the individual components of these embeddings are not redundant.

The Barlow Twins loss function is designed to achieve this objective. It is formulated based on the cross-correlation matrix of the outputs from the two networks.

Cross-Correlation Matrix Calculation:

Let's say the outputs (embeddings) from the two networks for a batch of samples are Y1 and Y2.
The cross-correlation matrix C is computed as the matrix product of the centered outputs of the two networks, normalized by the batch size.

Loss Function:

The diagonal elements of the matrix C represent the correlation of each component with itself. The method aims to make these diagonal elements equal to 1, ensuring that the embeddings from the two networks are similar.
The off-diagonal elements represent the correlation between different components. The method aims to make these off-diagonal elements equal to 0, ensuring that the components of the embeddings are not redundant.
The loss is then computed as the sum of the squared differences between the diagonal elements and the squared values of the off-diagonal elements.

Pseudocode for Barlow Twins

The Barlow Twins approach can be applied to more complex datasets and tasks beyond simple image classification. The key idea is to leverage the structure in unlabeled data by ensuring that the learned representations are consistent across distortions and non-redundant.

Redundancy Reduction Principle

Horace Basil Barlow, a renowned British vision scientist, significantly contributed to our understanding of the visual system. One of his most influential concepts was the redundancy reduction principle. Barlow posited that one of the primary computational aims of the visual system is to reduce redundancy, leading to the efficient coding hypothesis4. In simpler terms, while adjacent points in images often have similar brightness levels, the retina minimizes this redundancy, ensuring that the information processed is as concise and non-redundant as possible.

The Barlow Twins method in self-supervised learning draws inspiration from this principle. By reducing redundancy, the Barlow Twins approach aims to create embeddings invariant to distortions and statistically independent across different parts of an image. This ensures that the neural networks, when trained with this method, produce representations that capture the essential features of the data while discarding superfluous information.

In machine learning and computer vision, applying Barlow's redundancy reduction principle through the Barlow Twins method offers a promising avenue for achieving state-of-the-art results in various tasks, from image classification to segmentation.

Key Features of Barlow Twins

Independence from Large Batches

One of the standout features of the Barlow Twins method is its independence from large batches. In deep learning, especially with extensive datasets, large batch sizes are often employed to expedite training. However, this can lead to challenges, including the need for significant GPU memory and potential generalization issues.

The Barlow Twins approach, in contrast, does not necessitate large batches. This independence is particularly advantageous for those without access to extensive computational resources. The method's design, which emphasizes measuring the cross-correlation matrix between the outputs of two identical networks fed with distorted versions of a sample, ensures that the embeddings produced are invariant to these distortions. By aiming to make this matrix as close to the identity matrix as possible, the Barlow Twins method effectively minimizes redundancy between the components of the embedding vectors, irrespective of the batch size.

Another noteworthy aspect is the method's resilience to overfitting. Since it doesn't rely on large batches, the risk of the model memorizing the training data, a common pitfall in machine learning, is substantially reduced. This ensures the trained models are more robust and can generalize to unseen data.

The Barlow Twins approach's design, emphasizing redundancy reduction and independence from large batches, sets it apart in self-supervised learning methods. Its unique features make it resource-efficient and ensure its applicability and effectiveness across various tasks and computational settings.

Symmetry in Network Twins

The Barlow Twins approach is distinctive in its utilization of two identical neural networks, often called "twins". This symmetry departs from many other self-supervised learning methods that rely on predictor networks, gradient stopping, or moving averages to achieve their objectives.

The beauty of this symmetric design lies in its simplicity and efficiency. By feeding distorted versions of a sample into these twin networks and then comparing their outputs, the Barlow Twins method ensures that the produced embeddings are invariant to the distortions. This symmetry eliminates the need for additional complexities like predictor networks, often used to map representations from one network to another.

The absence of gradient stopping and moving averages in the Barlow Twins approach means that the training process is more straightforward and less prone to potential pitfalls associated with these techniques. Gradient stopping, for instance, can sometimes hinder the optimization process, leading to suboptimal results.

In essence, the symmetric design of the Barlow Twins method not only simplifies the training process but also enhances the robustness and effectiveness of the learned representations. By focusing on redundancy reduction and leveraging the power of symmetric network twins, the Barlow Twins approach offers a fresh perspective in the ever-evolving landscape of self-supervised learning.

Benefits of High-Dimensional Output Vectors

The Barlow Twins approach has garnered attention for its unique take on self-supervised learning, particularly in its use of high-dimensional output vectors. But why does this matter?

High-dimensional vectors allow for a richer data representation in neural networks. The Barlow Twins method can capture intricate patterns and nuances in the data that might be missed with lower-dimensional representations when using very high-dimensional vectors. This depth of representation is crucial for tasks like image recognition in computer vision, where subtle differences can be the key to accurate classification.

Moreover, the Barlow Twins method leverages these high-dimensional vectors to ensure that the embeddings produced by the twin networks are both similar (due to the distorted versions of a sample) and minimally redundant. This balance between similarity and non-redundancy is achieved through the redundancy reduction principle, inspired by neuroscientist H. Barlow.

To illustrate, imagine describing a complex painting using only a few colors. While you might capture the general theme, many details must be recovered. Now, imagine having a vast palette of colors at your disposal. The richness and depth of your description would be incomparably better. Similarly, high-dimensional vectors offer a richer "palette" for neural networks to represent data.

Using very high-dimensional vectors in the Barlow Twins method allows for a more detailed and nuanced understanding of data, paving the way for more accurate and robust machine learning models.

Performance and Comparisons

The Barlow Twins approach has been a significant leap forward in self-supervised learning, particularly when benchmarked against the ImageNet dataset.13 ImageNet is a large-scale dataset pivotal for computer vision tasks and is a rigorous testing ground for novel algorithms and methodologies.

In semi-supervised classification, especially in scenarios where data is limited, the Barlow Twins method has showcased commendable performance. The method outperforms previous methods on ImageNet for semi-supervised classification in the low-data regime. This is particularly noteworthy as working with limited data often challenges training robust models. With its unique approach to redundancy reduction and high-dimensional output vectors, the Barlow Twins method captures intricate patterns in the data, leading to improved classification results.

Moreover, using a linear classifier head, the Barlow Twins approach aligns with the current state-of-the-art ImageNet classification. It also holds its ground in transfer tasks of classification and object detection.13 These results underscore the potential of the Barlow Twins method in pushing the boundaries of self-supervised learning, especially in computer vision tasks.

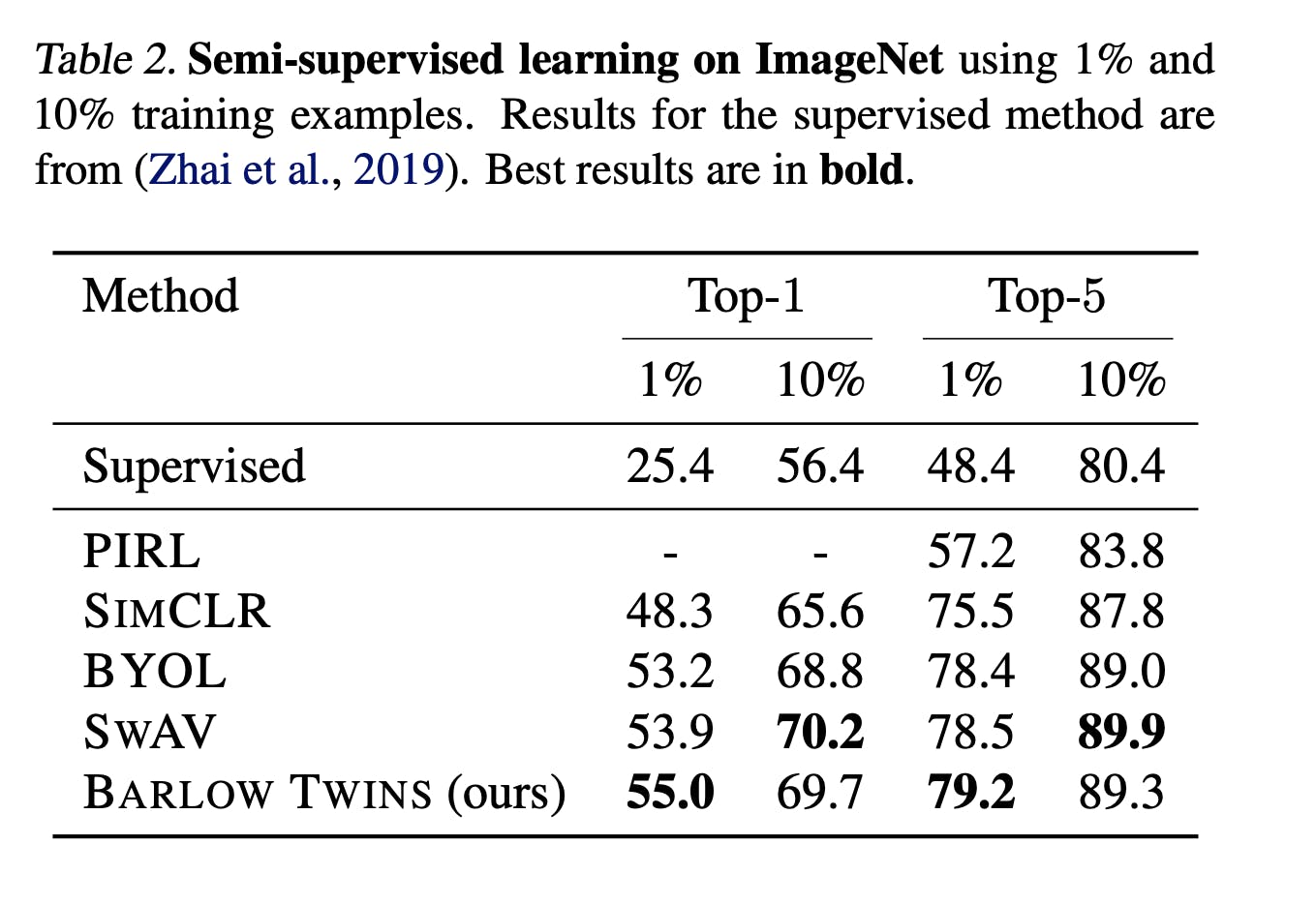
ImageNet numbers for Barlow Twin SSL approach

The Barlow Twins approach to SSL focuses on learning embeddings that remain invariant to input sample distortions. A significant challenge in this domain has been the emergence of trivial, constant solutions. While most contemporary methods have circumvented this issue through meticulous implementation nuances, the Barlow Twins approach introduces an objective function that inherently prevents such collapses.6

The Barlow Twins algorithm exhibits certain features when combined with other SSL methods. For instance, SimCLR and BYOL, two state-of-the-art SSL baselines, rely heavily on negative samples and data augmentations, respectively. In contrast, the Barlow Twins method sidesteps the need for negative samples, focusing instead on minimizing the redundancy between embeddings. This approach, combined with large batches and a tailored learning rate, has been instrumental in its success.

Furthermore, the Barlow Twins algorithm has been tested on the ImageNet dataset, a large-scale computer vision benchmark. The results were compelling. Using a ResNet-50 encoder and a projector network, the Barlow Twins achieved a 67.9% top-1 accuracy after 100 epochs. This performance is particularly noteworthy when considering the algorithm's simplicity and the projector network's absence of batch normalization or ReLU.

It's worth noting that the Barlow Twins' performance and comparisons are actively discussed on various platforms, including GitHub, where developers and researchers share their insights and modifications to the algorithm. As the field of SSL continues to grow, it will be intriguing to see how the Barlow Twins evolve and where they stand across different SSL methods.

Barlow Twins: Key Takeaways

The Importance of Redundancy Reduction

The Barlow Twins method has been recognized for its innovative application of the Redundancy Reduction principle in self-supervised learning (SSL).6 This principle, inspired by neuroscientist H. Barlow, emphasizes the significance of reducing redundant information while retaining essential features. In the context of the Barlow Twins, this means creating embeddings invariant to distortions of the input sample while avoiding trivial constant solutions. The method achieves this by measuring the cross-correlation matrix between the outputs of two identical networks fed with distorted versions of a sample and ensuring it remains close to the identity matrix. This intricate balance ensures that the embeddings of distorted versions of a sample are alike, yet the redundancy between the components of these vectors is minimized.

Advantages Over Other SSL Methods

The Barlow Twins approach offers several unique advantages over other SSL methods. One of its standout features is its ability to naturally avoid the collapse of embeddings without needing large batches or asymmetry between the twin networks. This is achieved without using techniques like gradient stopping, predictor networks, or moving averages on weight updates. Furthermore, the method benefits from high-dimensional output vectors, allowing for richer data representation and improved performance in tasks like image recognition.

The future looks promising as SSL narrows the gap with supervised methods, especially in large computer vision benchmarks. With its unique approach and advantages, the Barlow Twins method is poised to play a pivotal role in developing SSL methods. The potential for further research lies in refining the method, exploring its application in diverse domains, and integrating it with other advanced techniques to push the boundaries in SSL.

Build better ML models with Encord

Get started today

Written by

Alexandre Bonnet

View more posts

Frequently asked questions

The Barlow Twins method is an approach in self-supervised learning (SSL) that aims to create embeddings invariant to distortions of the input sample. The method is named after neuroscientist H. Barlow, who proposed the redundancy-reduction principle. In the context of Barlow Twins, this principle is applied to measure the cross-correlation matrix between the outputs of two identical networks fed with distorted versions of a sample. The objective is to make this matrix as close to the identity matrix as possible, ensuring that the embeddings of distorted versions of a sample are similar while minimizing redundancy between the components of these vectors.
The Barlow Twins method is not strictly a contrastive learning method. While both approaches aim to learn representations by comparing different views of the same data, Barlow Twins focuses on reducing redundancy between the components of the output vectors of two identical networks. It does this by ensuring the cross-correlation matrix of the outputs remains close to the identity matrix.
Both VICReg and Barlow Twins are methods in self-supervised learning, but they have distinct objectives and mechanisms. While Barlow Twins emphasizes reducing redundancy by aligning the cross-correlation matrix of twin network outputs with the identity matrix, VICReg might have different objectives and techniques to achieve its goals. The differences require a detailed comparison of both methods, available in dedicated research papers or comparative studies.

Previous blog

Image Thresholding in Image Processing

Next blog

Introduction to Vision Transformers (ViT)

May 11 2023

5 M

machine learning

machine learning

Guide to Image Segmentation in Computer Vision: Best Practices

Image segmentation is a crucial task in computer vision, where the goal is to divide an image into different meaningful and distinguishable regions or objects. It is a fundamental task in various applications such as object recognition, tracking, and detection, medical imaging, and robotics. Many techniques are available for image segmentation, ranging from traditional methods to deep learning-based approaches. With the advent of deep learning, the accuracy and efficiency of image segmentation have improved significantly. In this guide, we will discuss the basics of image segmentation, including different types of segmentation, applications, and various techniques used for image segmentation, including traditional, deep learning, and foundation model techniques. We will also cover evaluation metrics and datasets for evaluating image segmentation algorithms and future directions in image segmentation. By the end of this guide, you will have a better understanding of image segmentation, its applications, and the various techniques used for segmenting images. This guide is for you if you are a data scientist, machine learning engineer or your team is considering using image segmentation as part of an artificial intelligence computer vision project. What is Image Segmentation? Image segmentation is the process of dividing an image into multiple meaningful and homogeneous regions or objects based on their inherent characteristics, such as color, texture, shape, or brightness. Image segmentation aims to simplify and/or change the representation of an image into something more meaningful and easier to analyze. Here, each pixel is labeled. All the pixels belonging to the same category have a common label assigned to them. The task of segmentation can further be done in two ways: Similarity: As the name suggests, the segments are formed by detecting similarity between image pixels. It is often done by thresholding (see below for more on thresholding). Machine learning algorithms (such as clustering) are based on this type of approach for image segmentation. Discontinuity: Here, the segments are formed based on the change of pixel intensity values within the image. This strategy is used by line, point, and edge detection techniques to obtain intermediate segmentation results that may be processed to obtain the final segmented image. Types of Segmentation Image segmentation modes are divided into three categories based on the amount and type of information that should be extracted from the image: Instance, semantic, and panoptic. Let’s look at these various modes of image segmentation methods. Also, to understand the three modes of image segmentation, it would be more convenient to know more about objects and backgrounds. Objects are the identifiable entities in an image that can be distinguished from each other by assigning unique IDs, while the background refers to parts of the image that cannot be counted, such as the sky, water bodies, and other similar elements. By distinguishing between objects and backgrounds, it becomes easier to understand the different modes of image segmentation and their respective applications. Instance Segmentation Instance segmentation is a type of image segmentation that involves detecting and segmenting each object in an image. It is similar to object detection but with the added task of segmenting the object’s boundaries. The algorithm has no idea of the class of the region, but it separates overlapping objects. Instance segmentation is useful in applications where individual objects need to be identified and tracked. Instance segmentation Semantic Segmentation Semantic segmentation is a type of image segmentation that involves labeling each pixel in an image with a corresponding class label with no other information or context taken into consideration. The goal is to assign a label to every pixel in the image, which provides a dense labeling of the image. The algorithm takes an image as input and generates a segmentation map where the pixel value (0,1,...255) of the image is transformed into class labels (0,1,...n). It is useful in applications where identifying the different classes of objects on the road is important. Semantic segmentation - the human and the dog are classified together as mammals and separated from the rest of the background. Panoptic Segmentation Panoptic segmentation is a combination of semantic and instance segmentation. It involves labeling each pixel with a class label and identifying each object instance in the image. This mode of image segmentation provides the maximum amount of high-quality granular information from machine learning algorithms. It is useful in applications where the computer vision model needs to detect and interact with different objects in its environment, like an autonomous robot. Panoptic segmentation Each type of segmentation has its unique characteristics and is useful in different applications. In the following section, let’s discuss the various applications of image segmentation. Image Segmentation Techniques Traditional Techniques Traditional image segmentation techniques have been used for decades in computer vision to extract meaningful information from images. These techniques are based on mathematical models and algorithms that identify regions of an image with common characteristics, such as color, texture, or brightness. Traditional image segmentation techniques are usually computationally efficient and relatively simple to implement. They are often used for applications that require fast and accurate segmentation of images, such as object detection, tracking, and recognition. In this section, we will explore some of the most common techniques. Thresholding Thresholding Thresholding is one of the simplest image segmentation methods. Here, the pixels are divided into classes based on their histogram intensity which is relative to a fixed value or threshold. This method is suitable for segmenting objects where the difference in pixel values between the two target classes is significant. In low-noise images, the threshold value can be kept constant, but with images with noise, dynamic thresholding performs better. In thresholding-based segmentation, the greyscale image is divided into two segments based on their relationship to the threshold value, producing binary images. Algorithms like contour detection and identification work on these binarized images. The two commonly used thresholding methods are: Global thresholding is a technique used in image segmentation to divide images into foreground and background regions based on pixel intensity values. A threshold value is chosen to separate the two regions, and pixels with intensity values above the threshold are assigned to the foreground region and those below the threshold to the background region. This method is simple and efficient but may not work well for images with varying illumination or contrast. In those cases, adaptive thresholding techniques may be more appropriate. Adaptive thresholding is a technique used in image segmentation to divide an image into foreground and background regions by adjusting the threshold value locally based on the image characteristics. The method involves selecting a threshold value for each smaller region or block, based on the statistics of the pixel values within that block. Adaptive thresholding is useful for images with non-uniform illumination or varying contrast and is commonly used in document scanning, image binarization, and image segmentation. The choice of adaptive thresholding technique depends on the specific application requirements and image characteristics. Image showing different thresholding techniques. Source: Author Region-based Segmentation Region-based segmentation is a technique used in image processing to divide an image into regions based on similarity criteria, such as color, texture, or intensity. The method involves grouping pixels into regions or clusters based on their similarity and then merging or splitting regions until the desired level of segmentation is achieved. The two commonly used region-based segmentation techniques are: Split and merge segmentation is a region-based segmentation technique that recursively divides an image into smaller regions until a stopping criterion is met and then merges similar regions to form larger regions. The method involves splitting the image into smaller blocks or regions and then merging adjacent regions that meet certain similarity criteria, such as similar color or texture. Split and merge segmentation is a simple and efficient technique for segmenting images, but it may not work well for complex images with overlapping or irregular regions. Graph-based segmentation is a technique used in image processing to divide an image into regions based on the edges or boundaries between regions. The method involves representing the image as a graph, where the nodes represent pixels, and the edges represent the similarity between pixels. The graph is then partitioned into regions by minimizing a cost function, such as the normalized cut or minimum spanning tree. Example of graph-based image segmentation. Source Edge-based Segmentation Edge-based segmentation is a technique used in image processing to identify and separate the edges of an image from the background. The method involves detecting the abrupt changes in intensity or color values of the pixels in the image and using them to mark the boundaries of the objects. The two most common edge-based segmentation techniques are: Canny edge detection is a popular method for edge detection that uses a multi-stage algorithm to detect edges in an image. The method involves smoothing the image using a Gaussian filter, computing the gradient magnitude and direction of the image, applying non-maximum suppression to thin the edges, and using hysteresis thresholding to remove weak edges. Example of canny edge detection Sobel edge detection is a method for edge detection that uses a gradient-based approach to detect edges in an image. The method involves computing the gradient magnitude and direction of the image using a Sobel operator, which is a convolution kernel that extracts horizontal and vertical edge information separately. Example of Sobel edge detection. Laplacian of Gaussian (LoG) edge detection is a method for edge detection that combines Gaussian smoothing with the Laplacian operator. The method involves applying a Gaussian filter to the image to remove noise and then applying the Laplacian operator to highlight the edges. LoG edge detection is a robust and accurate method for edge detection, but it is computationally expensive and may not work well for images with complex edges. Example of Laplacian of Gaussian edge detection. Clustering Clustering is one of the most popular techniques used for image segmentation, as it can group pixels with similar characteristics into clusters or segments. The main idea behind clustering-based segmentation is to group pixels into clusters based on their similarity, where each cluster represents a segment. This can be achieved using various clustering algorithms, such as K means clustering, mean shift clustering, hierarchical clustering, and fuzzy clustering. K-means clustering is a widely used clustering algorithm for image segmentation. In this approach, the pixels in an image are treated as data points, and the algorithm partitions these data points into K clusters based on their similarity. The similarity is measured using a distance metric, such as Euclidean distance or Mahalanobis distance. The algorithm starts by randomly selecting K initial centroids, and then iteratively assigns each pixel to the nearest centroid and updates the centroids based on the mean of the assigned pixels. This process continues until the centroids converge to a stable value. ‍ Showing the result of segmenting the image at k=2,4,10. Source Mean shift clustering is another popular clustering algorithm used for image segmentation. In this approach, each pixel is represented as a point in a high-dimensional space, and the algorithm shifts each point toward the direction of the local density maximum. This process is repeated until convergence, where each pixel is assigned to a cluster based on the nearest local density maximum. Source ‍Though these techniques are simple, they are fast and memory efficient. But these techniques are more suitable for simpler segmentation tasks as well. They often require tuning to customize the algorithm as per the use case and also provide limited accuracy on complex scenes. Deep Learning Techniques Neural networks also provide solutions for image segmentation by training neural networks to identify which features are important in an image, rather than relying on customized functions like in traditional algorithms. Neural nets that perform the task of segmentation typically use an encoder-decoder structure. The encoder extracts features of an image through narrower and deeper filters. If the encoder is pre-trained on a task like an image or face recognition, it then uses that knowledge to extract features for segmentation (transfer learning). The decoder then over a series of layers inflates the encoder’s output into a segmentation mask resembling the pixel resolution of the input image. The basic architecture of the neural network model for image segmentation. Source ‍ Many deep learning models are quite adept at performing the task of segmentation reliably. Let’s have a look at a few of them: U-Net U-Net is a modified, fully convolutional neural network. It was primarily proposed for medical purposes, i.e., to detect tumors in the lungs and brain. It has the same encoder and decoder. The encoder is used to extract features using a shortcut connection, unlike in fully convolutional networks, which extract features by upsampling. The shortcut connection in the U-Net is designed to tackle the problem of information loss. In the U-Net architecture, the encoders and decoders are designed in such a manner that the network captures finer information and retains more information by concatenating high-level features with low-level ones. This allows the network to yield more accurate results. U-Net Architecture. Source‍ SegNet SegNet is also a deep fully convolutional network that is designed especially for semantic pixel-wise segmentation. Like U-Net, SegNet’s architecture also consists of encoder and decoder blocks. The SegNet differs from other neural networks in the way it uses its decoder for upsampling the features. The decoder network uses the pooling indices computed in the max-pooling layer which in turn makes the encoder perform non-linear upsampling. This eliminates the need for learning to upsample. SegNet is primarily designed for scene-understanding applications. SegNet Architecture. Source DeepLab DeepLab is primarily a convolutional neural network (CNN) architecture. Unlike the other two networks, it uses features from every convolutional block and then concatenates them to their deconvolutional block. The neural network uses the features from the last convolutional block and upsamples it like the fully convolutional network (FCN). It uses the atrous convolution or dilated convolution method for upsampling. The advantage of atrous convolution is that the computation cost is reduced while capturing more information. The encoder-Decoder architecture of DeepLab v3. Source Foundation Model Techniques Foundation models have also been used for image segmentation, which divides an image into distinct regions or segments. Unlike language models, which are typically based on transformer architectures, foundation models for image segmentation often use convolutional neural networks (CNNs) designed to handle image data. Segment Anything Model Segment Anything Model (SAM) is considered the first foundation model for image segmentation. SAM is built on the largest segmentation dataset to date, with over 1 billion segmentation masks. It is trained to return a valid segmentation mask for any prompt, where a prompt can be foreground/background points, a rough box or mask, freeform text, or general information indicating what to segment in an image. Under the hood, an image encoder produces a one-time embedding for the image, while a lightweight encoder converts any prompt into an embedding vector in real time. These two information sources are combined in a lightweight decoder that predicts segmentation masks.‍ Source Metrics for Evaluating Image Segmentation Algorithms Pixel Accuracy Pixel accuracy is a common evaluation metric used in image segmentation to measure the overall accuracy of the segmentation algorithm. It is defined as the ratio of the number of correctly classified pixels to the total number of pixels in the image. Pixel accuracy is a straightforward and easy-to-understand metric that provides a quick assessment of the segmentation performance. However, it does not account for the spatial alignment between the ground truth and the predicted segmentation, which can be important in some applications. In addition, pixel accuracy can be sensitive to class imbalance, where one class has significantly more pixels than another. This can lead to a biased evaluation of the algorithm's performance. Dice Coefficient The dice coefficient measures the similarity between two sets of binary data, in this case, the ground truth segmentation and the predicted segmentation. The dice coefficient is calculated as Where intersection is the number of pixels that are correctly classified as positive by both the ground truth and predicted segmentations, and ground truth and predicted are the total number of positive pixels in the respective segmentations. The Dice coefficient ranges from 0 to 1, with higher values indicating better segmentation performance. A value of 1 indicates a perfect overlap between the ground truth and predicted segmentations. The Dice coefficient is a popular metric for image segmentation because it is sensitive to small changes in the segmentation and is not affected by class imbalance. However, it does not account for the spatial alignment between the ground truth and predicted segmentation, which can be important in some applications. Jaccard Index (IOU) The Jaccard index, also known as the intersection over union (IoU) score, measures the similarity between the ground truth segmentation and the predicted segmentation. It is formulated as Where intersection is the number of pixels that are correctly classified as positive by both the ground truth and predicted segmentations, and ground truth and predicted are the total number of positive pixels in the respective segmentations. The IoU score ranges from 0 to 1, with higher values indicating better segmentation performance. A value of 1 indicates a perfect overlap between the ground truth and predicted segmentations. The Jaccard index takes into account both the true positives and false positives and is not affected by class imbalance. It also accounts for the spatial alignment between the ground truth and predicted segmentations. Datasets for Evaluating Image Segmentation Algorithms The evaluation of image segmentation algorithms is a crucial task n computer vision research. To measure the performance of these algorithms, various benchmark datasets have been developed. We will be discussing three popular datasets for evaluating image segmentation algorithms. These datasets provide carefully annotated images with pixel-level annotations, allowing researchers to test and compare the effectiveness of their segmentation algorithms. Barkley Segmentation Dataset and Benchmark The Barkley Segmentation Dataset is a standard benchmark for contour detection. This dataset is intended for testing natural edge detection, which takes into account background boundaries in addition to object interior and exterior boundaries as well as object contours. It includes 500 natural images with carefully annotated boundaries collected from multiple users. The dataset is divided into three parts: 200 for training, 100 for validation, and the rest 200 for testing. Pascal VOC Segmentation Dataset The Pascal VOC Segmentation Dataset is a popular benchmark dataset for evaluating image segmentation algorithms. It contains images from 20 object categories and provides pixel-level annotations for each image. The dataset is divided into the train, validation, and test sets, with the test set used to evaluate the performance of segmentation algorithms. The Pascal VOC Segmentation Dataset has been used as a benchmark for various computer vision challenges, including the Pascal VOC Challenge and the COCO Challenge. MS COCO Segmentation Dataset The Microsoft Common Objects in Context (COCO) Segmentation Dataset is another widely used dataset for evaluating image segmentation algorithms. It contains over 330,000 images with object annotations, including segmentations of 80 object categories. The dataset is divided into the train, validation, and test sets, with the test set containing around 5,000 images. The MS COCO Segmentation Dataset is often used as a benchmark for evaluating segmentation algorithms in various computer vision challenges, including the COCO Challenge. Future Direction of Image Segmentation Auto-Segmentation with SAM Auto-segmentation refers to the process of automatically segmenting an image without human intervention. Auto-segmentation with Meta’s Segment Anything Model (SAM) has instantly become popular as it shows remarkable performance in image segmentation tasks. It is a single model that can easily perform both interactive segmentation and automatic segmentation. Since SAM is trained on a diverse, high-quality dataset, it can generalize to new types of objects and images beyond what is observed during training. This ability to generalize means that by and large, practitioners will no longer need to collect their segmentation data and fine-tune a model for their use case. Improvement in segmentation accuracy Improving segmentation accuracy is one of the main goals of researchers in the field of computer vision. Accurate segmentation is essential for various applications, including medical imaging, object recognition, and autonomous vehicles. While deep learning techniques have led to significant improvements in segmentation accuracy in recent years, there is still much room for improvement. Here are some ways researchers are working to improve segmentation accuracy: Incorporating additional data sources: One approach to improving segmentation accuracy is incorporating additional data sources beyond the raw image data. For example, depth information can provide valuable cues for object boundaries and segmentation, particularly in complex scenes with occlusions and clutter. Developing new segmentation algorithms: Researchers continuously develop new algorithms for image segmentation that can improve accuracy. For example, some recent approaches use adversarial training or reinforcement learning to refine segmentation results. Improving annotation quality: The quality of the ground truth annotations used to train segmentation algorithms is essential to achieving high accuracy. Researchers are working to improve annotation quality through various means, including incorporating expert knowledge and utilizing crowdsourcing platforms. Refining evaluation metrics: Evaluation metrics play a crucial role in measuring the accuracy of segmentation algorithms. Researchers are exploring new evaluation metrics beyond the traditional Dice coefficient and Jaccard index, such as the Boundary F1 score, which can better capture the quality of object boundaries. Integrate Deep Learning with Traditional Techniques While deep learning techniques have shown remarkable performance in segmentation tasks, traditional techniques such as clustering, thresholding, and morphological operations can still provide useful insights and improve accuracy. Here are some ways researchers are integrating deep learning with traditional techniques in image segmentation: Hybrid models: Researchers are developing hybrid models that combine deep learning with traditional techniques. For example, some approaches use clustering or thresholding to initialize deep learning models or post-process segmentation results. Multi-stage approaches: Multi-stage approaches involve using deep learning for initial segmentation and then refining the results using traditional techniques. For example, some approaches use morphological operations to smooth and refine segmentation results. Attention-based models: Attention-based models are a type of deep learning model that incorporates traditional techniques for computing attention weights within a feature map. Attention-based models can improve accuracy by focusing on relevant image features and ignoring irrelevant ones. Transfer learning: Transfer learning involves pretraining deep learning models on large datasets and then fine-tuning them for specific segmentation tasks. Traditional techniques such as clustering or thresholding can be used to identify relevant features for transfer learning. Applications of Image Segmentation Image segmentation has a wide range of applications in various fields, including medical imaging, robotics, autonomous vehicles, and surveillance. Here are some examples of how image segmentation is used in different fields: Medical imaging: Image segmentation is widely used in medical imaging for tasks such as tumor detection, organ segmentation, and disease diagnosis. Accurate segmentation is essential for treatment planning and monitoring disease progression. Robotics: Image segmentation is used in robotics for object recognition and manipulation. For example, robots can use segmentation to recognize and grasp specific objects, such as tools or parts, in industrial settings. Autonomous vehicles: Image segmentation is essential for the development of autonomous vehicles, allowing them to detect and classify objects in their environment, such as other vehicles, pedestrians, and obstacles. Accurate segmentation is crucial for safe and reliable autonomous navigation. Surveillance: Image segmentation is used in surveillance for detecting and tracking objects and people in real-time video streams. Segmentation can help to identify and classify objects of interest, such as suspicious behavior or potential threats. Agriculture: Image segmentation is used in agriculture for crop monitoring, disease detection, and yield prediction. Accurate segmentation can help farmers make informed decisions about crop management and optimize crop yields. Art and design: Image segmentation is used in art and design for tasks such as image manipulation, color correction, and style transfer. Segmentation can help to separate objects or regions of an image and apply different effects or modifications to them. Image Segmentation: Key Takeaways Image segmentation is a powerful technique that allows us to identify and separate different objects or regions within an image. It has a wide range of applications in fields such as medical imaging, robotics, and computer vision. In this guide, we covered various image segmentation techniques, including traditional techniques such as thresholding, region-based segmentation, edge-based segmentation, and clustering, as well as deep learning and foundation model techniques. We also discussed different evaluation metrics and datasets used to evaluate segmentation algorithms. As image segmentation continues to advance, future directions will focus on improving segmentation accuracy, integrating deep learning with traditional techniques, and exploring new applications in various fields. Auto-segmentation with the Segment Anything Model (SAM) is a promising direction that can reduce manual intervention and improve accuracy. Integration of deep learning with traditional techniques can also help to overcome the limitations of individual techniques and improve overall performance. With ongoing research and development, we can expect image segmentation to continue to make significant contributions to various fields and industries. Further Reading on Image Segmentation Comparing Two Object Segmentation Models: Mask-RCNN vs. Personalized-SAM Deep Learning Techniques for Medical Image Segmentation: Achievements and Challenges Visual Segmentation of “Simple” Objects for Robots Best practices in deep learning based segmentation of microscopy image Image segmentation: Papers with code

Nov 07 2022

15 M

Software To Help You Turn Your Data Into AI

Forget fragmented workflows, annotation tools, and Notebooks for building AI applications. Encord Data Engine accelerates every step of taking your model into production.