How does the Adam optimizer differ from other optimization algorithms?

The Adam optimizer combines the advantages of two popular optimization algorithms: AdaGrad and RMSProp. It adjusts the learning rate for each parameter and maintains an exponentially decaying average of past gradients.

Why is overfitting a concern in machine learning?

Overfitting occurs when a model performs exceptionally well on the training data but poorly on unseen data. It indicates that the model has become too complex and has memorized the training data rather than generalizing it.

How does regularization prevent overfitting?

Regularization techniques, like L1 and L2, add a penalty to the loss function. This penalty discourages overly complex models, which can lead to overfitting by adding a cost to the model's complexity.

What's the difference between model parameters and hyperparameters?

Model parameters are learned from the data during training, such as weights in a neural network. Hyperparameters, however, are set before training and guide the training process, like the learning rate.

Why is the learning rate crucial in the Adam optimizer?

Model parameters are learned from the data during training, such as weights in a neural network. Hyperparameters, however, are set before training and guide the training process, like the learning rate.

What is the curse of dimensionality in hyperparameter optimization?

As the number of hyperparameters increases, the search space grows exponentially, making the optimization process computationally expensive and time-consuming.

How does model complexity relate to its number of parameters?

A model's complexity increases with its number of parameters. While a complex model can capture intricate patterns, it's more susceptible to overfitting.

Are there alternatives to the Adam optimizer for hyperparameter optimization?

Yes, there are several optimization algorithms like SGD (Stochastic Gradient Descent), RMSProp, and AdaGrad, each with its advantages and use cases.

How can one decide which hyperparameters to prioritize during optimization?

Start with the most commonly tuned hyperparameters. For instance, neural networks often prioritize the learning rate and regularization parameters. Domain knowledge and experience also play a crucial role in this decision-making.

Back to Blogs

Contents

What is Hyperparameter Optimization?
Techniques for Hyperparameter Optimization
The Role of Adam Optimizer Hyperparameters
Challenges in Hyperparameter Optimization
Hyperparameter Optimization: Key Takeaways

Encord Blog

Fine-tuning Models: Hyperparameter Optimization

August 22, 2023

5 mins

Back to Blogs

Contents

What is Hyperparameter Optimization?
Techniques for Hyperparameter Optimization
The Role of Adam Optimizer Hyperparameters
Challenges in Hyperparameter Optimization
Hyperparameter Optimization: Key Takeaways

Written by

Alexandre Bonnet

View more posts

Hyperparameter optimization is a key concept in machine learning. At its core, it involves systematically exploring the most suitable set of hyperparameters that can elevate the performance of a model. These hyperparameters, distinct from model parameters, aren't inherently learned during the training phase. Instead, they're predetermined. Their precise configuration can profoundly sway the model's outcome, bridging the gap between an average model and one that excels.

Fine-tuning models delves into the meticulous process of refining a pre-trained model to better align with a specific task. Imagine the precision required in adjusting a musical instrument to hit the right notes; that's what fine-tuning achieves for models. It ensures they resonate perfectly with the data they're presented. The model learns at its maximum potential when hyperparameter optimization and fine-tuning converge. This union guarantees that machine learning models function and thrive, delivering unparalleled performance.

The role of tools like the Adam optimizer in this journey cannot be understated. As one of the many techniques in the hyperparameter optimization toolkit, it exemplifies the advancements in the field, offering efficient and effective ways to fine-tune models to perfection.

Label data 10x faster and gain control of your training data

Clean & curate data smartly

Create quality labels quickly

Validate your label quality

Evaluate & monitor your models

Book a live demo

This article will cover:

What is Hyperparameter Optimization?
Techniques for Hyperparameter Optimization.
The Role of Adam Optimizer
Challenges in Hyperparameter Optimization.

Diagram illustrating hyperparameter optimization process

What is Hyperparameter Optimization?

With its vast potential and intricate mechanisms, machine learning often hinges on fine details. One such detail pivotal to the success of a model is hyperparameter optimization. At its core, this process systematically searches for the best set of hyperparameters to elevate a model's performance.

But what distinguishes hyperparameters from model parameters? Model parameters are the model's aspects learned from the data during training, such as weights in a neural network. Hyperparameters, on the other hand, are set before training begins. They dictate the overarching structure and behavior of a model. They are adjusted settings or dials to optimize the learning process. This includes the learning rate, which determines how quickly a model updates its parameters in response to the training data, or the regularization term, which helps prevent overfitting.4

The challenge of hyperparameter optimization is monumental. Given the vastness of the hyperparameter space, with an almost infinite number of combinations, finding the optimal set is like searching for a needle in a haystack.

Techniques such as grid search, where a predefined set of hyperparameters is exhaustively tried, or random search, where hyperparameters are randomly sampled, are often employed. More advanced methods like Bayesian optimization, which builds a probabilistic model of the function mapping from hyperparameter values to the objective value, are also gaining traction.5

Build Better Models, Faster with Encord's Leading Annotation Tool

Why Fine-tuning is Essential

The configuration and hyperparameter tuning can profoundly influence a model's performance. A slight tweak can be the difference between a mediocre outcome and stellar results. For instance, the Adam optimizer, a popular **optimization method** in deep learning, has specific hyperparameters that, when fine-tuned, can lead to faster and more stable convergence during training. 6

In real-world applications, hyperparameter search and fine-tuning become even more evident. Consider a scenario where a pre-trained neural network, initially designed for generic image recognition, is repurposed for a specialized task like medical image analysis. Its accuracy and reliability can be significantly enhanced by searching for optimal hyperparameters and fine-tuning them for this dataset. This could mean distinguishing between accurately detecting a medical anomaly and missing it altogether.

Furthermore, as machine learning evolves, our datasets and challenges become more complex. In such a landscape, the ability to fine-tune models and optimize hyperparameters using various optimization methods is not just beneficial; it's essential. It ensures that our models are accurate, efficient, adaptable, and ready to tackle the challenges of tomorrow.

Techniques for Hyperparameter Optimization

Hyperparameter optimization focuses on finding the optimal set of hyperparameters for a given model. Unlike model parameters, these hyperparameters are not learned during training but are set before the training begins. Their correct setting can significantly influence the model's performance.

Grid Search

Grid Search involves exhaustively trying out every possible combination of hyperparameters in a predefined search space. For instance, if you're fine-tuning a model and considering two hyperparameters, learning rate and batch size, a grid search would test all combinations of the values you specify for these hyperparameters.

Let's consider classifying images of handwritten digits (a classic problem known as the MNIST classification). Here, the images are 28x28 pixels, and the goal is to classify them into one of the ten classes (0 through 9).

For an SVM applied to this problem, two critical hyperparameters are:

The type and parameters of the kernel: For instance, if using the Radial Basis Function (RBF) kernel, we need to determine the gamma value.
The regularization parameter (C) determines the trade-off between maximizing the margin and minimizing classification error.

Using grid search, we can systematically explore combinations of:

Different kernels: linear, polynomial, RBF, etc.
Various values of gamma (for RBF): e.g., [0.1, 1, 10, 100]
Different values of C: e.g., [0.1, 1, 10, 100]

By training the SVM with each combination and validating its performance on a separate dataset, grid search allows us to pinpoint the combination that yields the best classification accuracy.

Advantages of Grid Search

Comprehensive: Since it tests all possible combinations, there's a high chance of finding the optimal set.
Simple to implement: It doesn't require complex algorithms or techniques.

Disadvantages of Grid Search

Computationally expensive: As the number of hyperparameters or their potential values increases, the number of combinations to test grows exponentially.
Time-consuming: Due to its exhaustive nature, it can be slow, especially with large datasets or complex models.

Random Search

Random Search, as the name suggests, involves randomly selecting and evaluating combinations of hyperparameters. Unlike Grid Search, which exhaustively tries every possible combination, Random Search samples a predefined number of combinations from a specified distribution for each hyperparameter. 11

Consider a scenario where a financial institution develops a machine learning model to predict loan defaults. The dataset is vast, with numerous features ranging from a person's credit history to current financial status.

The model in question, a deep neural network, has several hyperparameters like learning rate, batch size, and the number of layers. Given the high dimensionality of the hyperparameter space, using Grid Search might be computationally expensive and time-consuming. By randomly sampling hyperparameter combinations, the institution can efficiently narrow down the best settings with the highest prediction accuracy, saving time and computational resources.13

Advantages of Random Search

Efficiency: Random Search can be more efficient than Grid Search, especially when the number of hyperparameters is large. It doesn't need to try every combination, which can save time.12
Flexibility: It allows for a more flexible specification of hyperparameters, as they can be drawn from any distribution, not just a grid.
Surprising Results: Sometimes, Random Search can stumble upon hyperparameter combinations that might be overlooked in a more structured search approach.

Disadvantages of Random Search

No Guarantee: There's no guarantee that Random Search will find the optimal combination of hyperparameters, especially if the number of iterations is too low.
Dependence on Iterations: The effectiveness of Random Search is highly dependent on the number of iterations. Too few iterations might miss the optimal settings, while too many can be computationally expensive.

Bayesian Optimization

Bayesian Optimization is a probabilistic model-based optimization technique particularly suited for optimizing expensive-to-evaluate and noisy functions. Unlike random or grid search, Bayesian Optimization builds a probabilistic model of the objective function. It uses it to select the most promising hyperparameters to evaluate the true objective function.

Bayesian Optimization shines in scenarios where the objective function is expensive to evaluate. For instance, training a model with a particular set of hyperparameters in deep learning can be time-consuming. Using grid search or random search in such scenarios can be computationally prohibitive. By building a model of the objective function, Bayesian Optimization can more intelligently sample the hyperparameter space to find the optimal set in fewer evaluations.

Bayesian Optimization is more directed than grid search, which exhaustively tries every combination of hyperparameters, or random search, which samples them randomly. It uses past evaluation results to choose the next set of hyperparameters to evaluate. This makes it particularly useful when evaluating the objective function (like training a deep learning model) is time-consuming or expensive.

However, it's worth noting that if the probabilistic model's assumptions do not align well with the true objective function, Bayesian Optimization might not perform as well. A more naive approach like random search might outperform it in such cases.1

Advantages of Bayesian Optimization

Efficiency: Bayesian Optimization typically requires fewer function evaluations than random or grid search, making it especially useful for optimizing expensive functions.
Incorporation of Prior Belief: It can incorporate prior beliefs about the function and then sequentially refine this model as more samples are collected.
Handling of Noisy Objective Functions: It can handle noisy objective functions, meaning that there's some random noise added to the function's output each time it's evaluated.

Disadvantages of Bayesian Optimization

Model Assumptions: The performance of Bayesian Optimization can be sensitive to the assumptions made by the probabilistic model.
Computationally Intensive: As the number of observations grows, the computational complexity of updating the probabilistic model and selecting the next sample point can become prohibitive.

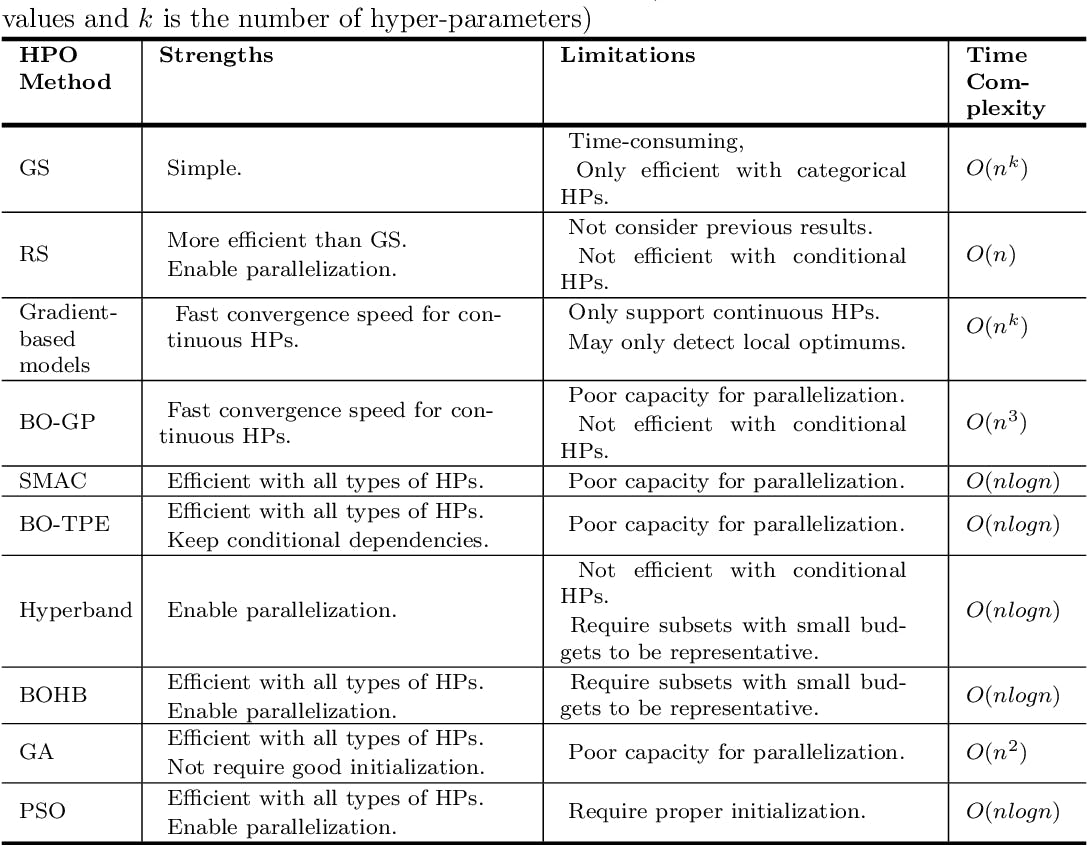
A comparison chart of different optimization techniques

The Role of Adam Optimizer Hyperparameters

The Adam optimizer has emerged as a popular choice for training deep learning models in the vast landscape of optimization algorithms. But what makes it so special? And how do its hyperparameters influence the fine-tuning process?

Introduction to the Adam Optimizer

The Adam optimizer, short for Adaptive Moment Estimation, is an optimization algorithm for training neural networks. It combines two other popular optimization techniques: AdaGrad and RMSProp. The beauty of Adam is that it maintains separate learning rates for each parameter and adjusts them during training. This adaptability makes it particularly effective for problems with sparse gradients, such as natural language processing tasks.5

Significance of Adam in Model Training

Adam has gained popularity due to its efficiency and relatively low memory requirements. Unlike traditional gradient descent, which maintains a single learning rate for all weight updates, Adam computes adaptive learning rates for each parameter. This means it can fine-tune models faster and often achieve better performance on test datasets. Moreover, Adam is less sensitive to hyperparameter settings, making it a more forgiving choice for those new to model training.. 7

Impact of Adam's Hyperparameters on Model Training

The Adam optimizer has three primary hyperparameters: the learning rate, beta1, and beta2. Let's break down their roles:

Learning Rate (α): This hyperparameter determines the step size at each iteration while moving towards a minimum in the loss function. A smaller learning rate might converge slowly, while a larger one might overshoot the minimum.
Beta1: This hyperparameter controls the exponential decay rate for the first-moment estimate. It's essentially a moving average of the gradients. A common value for beta1 is 0.9, which means the algorithm retains 90% of the previous gradient's value.8
Beta2 controls the exponential decay rate for the second moment estimate, an uncentered moving average of the squared gradient. A typical value is 0.999. 8

Fine-tuning these hyperparameters can significantly impact model training. For instance, adjusting the learning rate can speed up convergence or prevent the model from converging. Similarly, tweaking beta1 and beta2 values can influence how aggressively the model updates its weights in response to the gradients.

Practical Tips for Fine-tuning with Adam

Start with a Smaller Learning Rate: While Adam adjusts the learning rate for each parameter, starting with a smaller global learning rate (e.g., 0.0001) can lead to more stable convergence, especially in the early stages of training.
Adjust Beta Values: The default values of beta1 = 0.9 and beta2 = 0.999 work well for many tasks. However, slightly adjusting specific datasets or model architectures can lead to faster convergence or better generalization.
Monitor Validation Loss: Always monitor your validation loss. If it starts increasing while the training loss continues to decrease, it might be a sign of overfitting. Consider using early stopping or adjusting your learning rate.
Warm-up Learning Rate: Gradually increasing the learning rate at the beginning of training can help stabilize the optimizer. This "warm-up" phase can prevent large weight updates that can destabilize the model early on.
Use Weight Decay: Regularization techniques like weight decay can help prevent overfitting, especially when training larger models or when the dataset is small.
Epsilon Value: While the default value of ε is usually sufficient, increasing it slightly can help with numerical stability in some cases.

Best Practices

Learning Rate Scheduling: Decreasing the learning rate as training can help achieve better convergence. Techniques like step decay or exponential decay can be beneficial.
Batch Normalization: Using batch normalization layers in your neural network can make the model less sensitive to the initialization of weights, aiding in faster and more stable training.
Gradient Clipping: For tasks like training RNNs, where gradients can explode, consider gradient clipping to prevent substantial weight updates.
Regular Checkpoints: Always save model checkpoints regularly. This helps in unexpected interruptions and allows you to revert to a previous state if overfitting occurs.

Adam optimizer is powerful and adaptive; understanding its intricacies and fine-tuning its hyperparameters can improve model performance. Following these practical tips and best practices ensures that your model trains efficiently and generalizes well to unseen data.

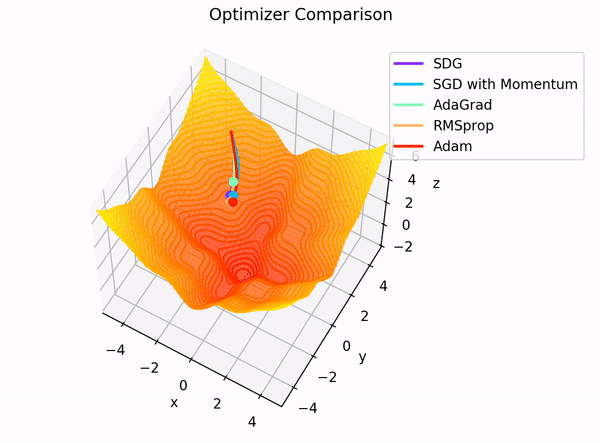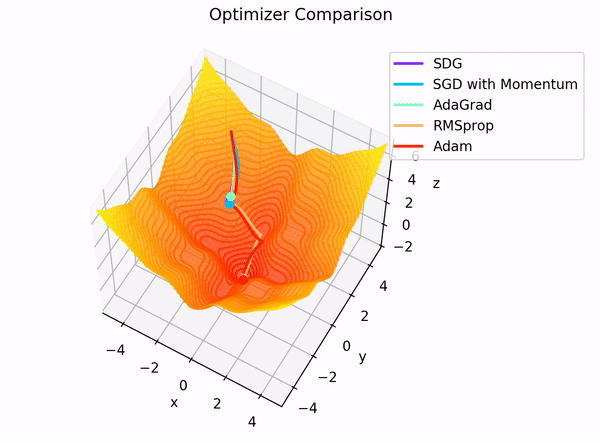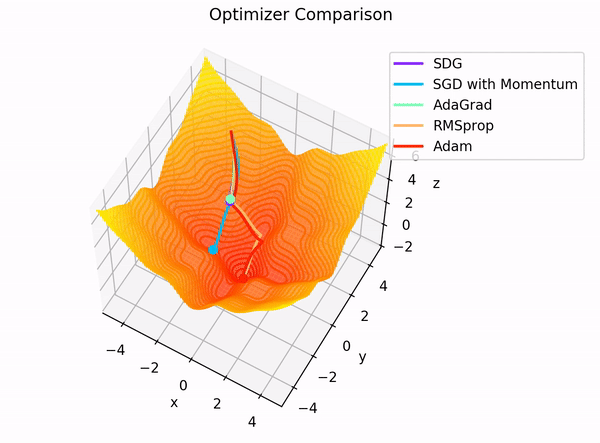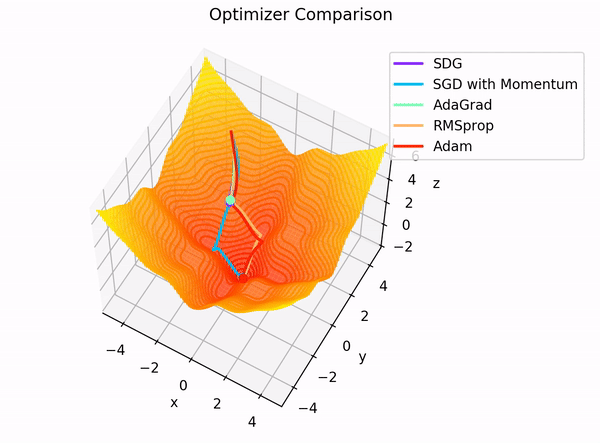
Visualization of Adam Optimizer in action

Challenges in Hyperparameter Optimization

Let's delve into common pitfalls practitioners face while choosing the best hyperparameters and explore strategies to overcome them.

The Curse of Dimensionality

When dealing with many hyperparameters, the search space grows exponentially. This phenomenon, known as the curse of dimensionality, can make the optimization process computationally expensive and time-consuming. 9

Strategy: One way to tackle this is by using dimensionality reduction techniques or prioritizing the most impactful hyperparameters.

Local Minima and Plateaus

Optimization algorithms can sometimes get stuck in local minima or plateaus, where further adjustments to hyperparameters don't significantly improve performance. 10

Strategy: Techniques like random restarts, where the optimization process is started from different initial points, or using more advanced optimization algorithms like Bayesian optimization, can help navigate these challenges.

Overfitting

Strategy: Regularization techniques, cross-validation, and maintaining a separate validation set can help prevent overfitting during hyperparameter optimization.

{{grey_callout_start}} For a deeper dive into data splitting techniques crucial for segregating the training set and test set, and playing a pivotal role in model training and validation, check out our detailed article on Train-Validation-Test Split. {{grey_callout_end}}

Computational Constraints

Hyperparameter optimization, especially grid search, can be computationally intensive. This becomes a challenge when resources are limited.

Strategy: Opt for more efficient search methods like random or gradient-based optimization, which can provide good results with less computational effort.

Lack of Clarity on Which Hyperparameters to Tune

Strategy: Start with the most commonly tuned hyperparameters. For instance, when fine-tuning models using the Adam optimizer, focus on learning and decay rates. 9

Hyperparameter optimization is essential for achieving the best model performance, and awareness of its challenges is crucial. By understanding these challenges and employing the strategies mentioned, practitioners can navigate the optimization process more effectively and efficiently.

Overfitting and Regularization

The Balance Between Model Complexity and Generalization

A model's complexity is directly related to its number of parameters. While a more complex model can capture intricate patterns in the training data, it's also more susceptible to overfitting.4 Conversely, a too-simple model might not capture the necessary patterns, leading to underfitting. The challenge lies in finding the sweet spot where the model is complex enough to learn from the training data but not so much that it loses its generalization ability.

Role of Hyperparameters in Preventing Overfitting

Hyperparameters can significantly influence a model's complexity. For instance, the number of layers and nodes in neural networks can determine how intricate patterns the model can capture.9 However, we can fine-tune this balance with the Adam optimizer and its hyperparameters.

The learning rate, one of the primary hyperparameters of the Adam optimizer, determines the step size at each iteration while moving towards a minimum of the loss function. A lower learning rate might make the model converge slowly, but it can also help avoid overshooting and overfitting. On the other hand, a larger learning rate might speed up the convergence. Still, it can cause the model to miss the optimal solution. 9

Regularization techniques, like L1 and L2 regularization, add a penalty to the loss function. By adjusting the regularization hyperparameter, one can control the trade-off between fitting the training data closely and keeping the model weights small to prevent overfitting.

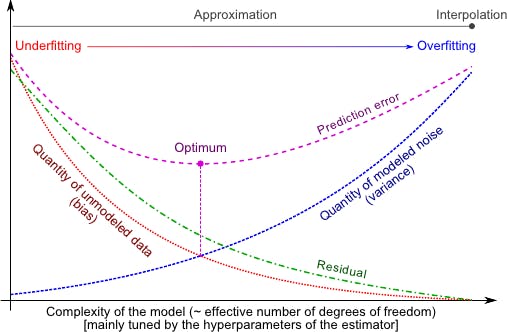
Graph illustrating overfitting and the role of hyperparameters

Hyperparameter Optimization: Key Takeaways

In the intricate landscape of machine learning, hyperparameter tuning and hyperparameter search are essential processes, ensuring that models achieve optimal performance through meticulous fine-tuning. The balance between model complexity and its generalization capability is paramount. The role of hyperparameters, especially within the framework of the Adam optimizer, is pivotal in maintaining this equilibrium and finding the optimal hyperparameters.

As machine learning continues to evolve, practitioners must remain aware of evolving methodologies and optimization methods. The hyperparameter optimization process is not a mere task but an ongoing commitment to refining models for superior outcomes.

It is, therefore, incumbent upon professionals in this domain to engage in rigorous experimentation and continual learning, ensuring that the models they develop are efficient, robust, and adaptable to the ever-evolving challenges presented by real-world data.

Build better ML models with Encord

Clean & curate data smartly

Create quality labels quickly

Validate your label quality

Evaluate & monitor your models

Book a live demo

Build better ML models with Encord

Get started today

Written by

Alexandre Bonnet

View more posts

Frequently asked questions

Hyperparameter optimization is systematically searching for the best set of hyperparameters that improves the performance of a machine learning model on a validation set.
The Adam optimizer combines the advantages of two popular optimization algorithms: AdaGrad and RMSProp. It adjusts the learning rate for each parameter and maintains an exponentially decaying average of past gradients.
Overfitting occurs when a model performs exceptionally well on the training data but poorly on unseen data. It indicates that the model has become too complex and has memorized the training data rather than generalizing it.
Regularization techniques, like L1 and L2, add a penalty to the loss function. This penalty discourages overly complex models, which can lead to overfitting by adding a cost to the model's complexity.
Model parameters are learned from the data during training, such as weights in a neural network. Hyperparameters, however, are set before training and guide the training process, like the learning rate.
Model parameters are learned from the data during training, such as weights in a neural network. Hyperparameters, however, are set before training and guide the training process, like the learning rate.
As the number of hyperparameters increases, the search space grows exponentially, making the optimization process computationally expensive and time-consuming.
A model's complexity increases with its number of parameters. While a complex model can capture intricate patterns, it's more susceptible to overfitting.
Yes, there are several optimization algorithms like SGD (Stochastic Gradient Descent), RMSProp, and AdaGrad, each with its advantages and use cases.
Start with the most commonly tuned hyperparameters. For instance, neural networks often prioritize the learning rate and regularization parameters. Domain knowledge and experience also play a crucial role in this decision-making.

Previous blog

Why AI Is the Mother of All Unicorns

Next blog

Part 2: Evaluating Foundation Models (CLIP) using Encord Active

May 11 2023

5 M

machine learning

machine learning

Guide to Image Segmentation in Computer Vision: Best Practices

Image segmentation is a crucial task in computer vision, where the goal is to divide an image into different meaningful and distinguishable regions or objects. It is a fundamental task in various applications such as object recognition, tracking, and detection, medical imaging, and robotics. Many techniques are available for image segmentation, ranging from traditional methods to deep learning-based approaches. With the advent of deep learning, the accuracy and efficiency of image segmentation have improved significantly. In this guide, we will discuss the basics of image segmentation, including different types of segmentation, applications, and various techniques used for image segmentation, including traditional, deep learning, and foundation model techniques. We will also cover evaluation metrics and datasets for evaluating image segmentation algorithms and future directions in image segmentation. By the end of this guide, you will have a better understanding of image segmentation, its applications, and the various techniques used for segmenting images. This guide is for you if you are a data scientist, machine learning engineer or your team is considering using image segmentation as part of an artificial intelligence computer vision project. What is Image Segmentation? Image segmentation is the process of dividing an image into multiple meaningful and homogeneous regions or objects based on their inherent characteristics, such as color, texture, shape, or brightness. Image segmentation aims to simplify and/or change the representation of an image into something more meaningful and easier to analyze. Here, each pixel is labeled. All the pixels belonging to the same category have a common label assigned to them. The task of segmentation can further be done in two ways: Similarity: As the name suggests, the segments are formed by detecting similarity between image pixels. It is often done by thresholding (see below for more on thresholding). Machine learning algorithms (such as clustering) are based on this type of approach for image segmentation. Discontinuity: Here, the segments are formed based on the change of pixel intensity values within the image. This strategy is used by line, point, and edge detection techniques to obtain intermediate segmentation results that may be processed to obtain the final segmented image. Types of Segmentation Image segmentation modes are divided into three categories based on the amount and type of information that should be extracted from the image: Instance, semantic, and panoptic. Let’s look at these various modes of image segmentation methods. Also, to understand the three modes of image segmentation, it would be more convenient to know more about objects and backgrounds. Objects are the identifiable entities in an image that can be distinguished from each other by assigning unique IDs, while the background refers to parts of the image that cannot be counted, such as the sky, water bodies, and other similar elements. By distinguishing between objects and backgrounds, it becomes easier to understand the different modes of image segmentation and their respective applications. Instance Segmentation Instance segmentation is a type of image segmentation that involves detecting and segmenting each object in an image. It is similar to object detection but with the added task of segmenting the object’s boundaries. The algorithm has no idea of the class of the region, but it separates overlapping objects. Instance segmentation is useful in applications where individual objects need to be identified and tracked. Instance segmentation Semantic Segmentation Semantic segmentation is a type of image segmentation that involves labeling each pixel in an image with a corresponding class label with no other information or context taken into consideration. The goal is to assign a label to every pixel in the image, which provides a dense labeling of the image. The algorithm takes an image as input and generates a segmentation map where the pixel value (0,1,...255) of the image is transformed into class labels (0,1,...n). It is useful in applications where identifying the different classes of objects on the road is important. Semantic segmentation - the human and the dog are classified together as mammals and separated from the rest of the background. Panoptic Segmentation Panoptic segmentation is a combination of semantic and instance segmentation. It involves labeling each pixel with a class label and identifying each object instance in the image. This mode of image segmentation provides the maximum amount of high-quality granular information from machine learning algorithms. It is useful in applications where the computer vision model needs to detect and interact with different objects in its environment, like an autonomous robot. Panoptic segmentation Each type of segmentation has its unique characteristics and is useful in different applications. In the following section, let’s discuss the various applications of image segmentation. Image Segmentation Techniques Traditional Techniques Traditional image segmentation techniques have been used for decades in computer vision to extract meaningful information from images. These techniques are based on mathematical models and algorithms that identify regions of an image with common characteristics, such as color, texture, or brightness. Traditional image segmentation techniques are usually computationally efficient and relatively simple to implement. They are often used for applications that require fast and accurate segmentation of images, such as object detection, tracking, and recognition. In this section, we will explore some of the most common techniques. Thresholding Thresholding Thresholding is one of the simplest image segmentation methods. Here, the pixels are divided into classes based on their histogram intensity which is relative to a fixed value or threshold. This method is suitable for segmenting objects where the difference in pixel values between the two target classes is significant. In low-noise images, the threshold value can be kept constant, but with images with noise, dynamic thresholding performs better. In thresholding-based segmentation, the greyscale image is divided into two segments based on their relationship to the threshold value, producing binary images. Algorithms like contour detection and identification work on these binarized images. The two commonly used thresholding methods are: Global thresholding is a technique used in image segmentation to divide images into foreground and background regions based on pixel intensity values. A threshold value is chosen to separate the two regions, and pixels with intensity values above the threshold are assigned to the foreground region and those below the threshold to the background region. This method is simple and efficient but may not work well for images with varying illumination or contrast. In those cases, adaptive thresholding techniques may be more appropriate. Adaptive thresholding is a technique used in image segmentation to divide an image into foreground and background regions by adjusting the threshold value locally based on the image characteristics. The method involves selecting a threshold value for each smaller region or block, based on the statistics of the pixel values within that block. Adaptive thresholding is useful for images with non-uniform illumination or varying contrast and is commonly used in document scanning, image binarization, and image segmentation. The choice of adaptive thresholding technique depends on the specific application requirements and image characteristics. Image showing different thresholding techniques. Source: Author Region-based Segmentation Region-based segmentation is a technique used in image processing to divide an image into regions based on similarity criteria, such as color, texture, or intensity. The method involves grouping pixels into regions or clusters based on their similarity and then merging or splitting regions until the desired level of segmentation is achieved. The two commonly used region-based segmentation techniques are: Split and merge segmentation is a region-based segmentation technique that recursively divides an image into smaller regions until a stopping criterion is met and then merges similar regions to form larger regions. The method involves splitting the image into smaller blocks or regions and then merging adjacent regions that meet certain similarity criteria, such as similar color or texture. Split and merge segmentation is a simple and efficient technique for segmenting images, but it may not work well for complex images with overlapping or irregular regions. Graph-based segmentation is a technique used in image processing to divide an image into regions based on the edges or boundaries between regions. The method involves representing the image as a graph, where the nodes represent pixels, and the edges represent the similarity between pixels. The graph is then partitioned into regions by minimizing a cost function, such as the normalized cut or minimum spanning tree. Example of graph-based image segmentation. Source Edge-based Segmentation Edge-based segmentation is a technique used in image processing to identify and separate the edges of an image from the background. The method involves detecting the abrupt changes in intensity or color values of the pixels in the image and using them to mark the boundaries of the objects. The two most common edge-based segmentation techniques are: Canny edge detection is a popular method for edge detection that uses a multi-stage algorithm to detect edges in an image. The method involves smoothing the image using a Gaussian filter, computing the gradient magnitude and direction of the image, applying non-maximum suppression to thin the edges, and using hysteresis thresholding to remove weak edges. Example of canny edge detection Sobel edge detection is a method for edge detection that uses a gradient-based approach to detect edges in an image. The method involves computing the gradient magnitude and direction of the image using a Sobel operator, which is a convolution kernel that extracts horizontal and vertical edge information separately. Example of Sobel edge detection. Laplacian of Gaussian (LoG) edge detection is a method for edge detection that combines Gaussian smoothing with the Laplacian operator. The method involves applying a Gaussian filter to the image to remove noise and then applying the Laplacian operator to highlight the edges. LoG edge detection is a robust and accurate method for edge detection, but it is computationally expensive and may not work well for images with complex edges. Example of Laplacian of Gaussian edge detection. Clustering Clustering is one of the most popular techniques used for image segmentation, as it can group pixels with similar characteristics into clusters or segments. The main idea behind clustering-based segmentation is to group pixels into clusters based on their similarity, where each cluster represents a segment. This can be achieved using various clustering algorithms, such as K means clustering, mean shift clustering, hierarchical clustering, and fuzzy clustering. K-means clustering is a widely used clustering algorithm for image segmentation. In this approach, the pixels in an image are treated as data points, and the algorithm partitions these data points into K clusters based on their similarity. The similarity is measured using a distance metric, such as Euclidean distance or Mahalanobis distance. The algorithm starts by randomly selecting K initial centroids, and then iteratively assigns each pixel to the nearest centroid and updates the centroids based on the mean of the assigned pixels. This process continues until the centroids converge to a stable value. ‍ Showing the result of segmenting the image at k=2,4,10. Source Mean shift clustering is another popular clustering algorithm used for image segmentation. In this approach, each pixel is represented as a point in a high-dimensional space, and the algorithm shifts each point toward the direction of the local density maximum. This process is repeated until convergence, where each pixel is assigned to a cluster based on the nearest local density maximum. Source ‍Though these techniques are simple, they are fast and memory efficient. But these techniques are more suitable for simpler segmentation tasks as well. They often require tuning to customize the algorithm as per the use case and also provide limited accuracy on complex scenes. Deep Learning Techniques Neural networks also provide solutions for image segmentation by training neural networks to identify which features are important in an image, rather than relying on customized functions like in traditional algorithms. Neural nets that perform the task of segmentation typically use an encoder-decoder structure. The encoder extracts features of an image through narrower and deeper filters. If the encoder is pre-trained on a task like an image or face recognition, it then uses that knowledge to extract features for segmentation (transfer learning). The decoder then over a series of layers inflates the encoder’s output into a segmentation mask resembling the pixel resolution of the input image. The basic architecture of the neural network model for image segmentation. Source ‍ Many deep learning models are quite adept at performing the task of segmentation reliably. Let’s have a look at a few of them: U-Net U-Net is a modified, fully convolutional neural network. It was primarily proposed for medical purposes, i.e., to detect tumors in the lungs and brain. It has the same encoder and decoder. The encoder is used to extract features using a shortcut connection, unlike in fully convolutional networks, which extract features by upsampling. The shortcut connection in the U-Net is designed to tackle the problem of information loss. In the U-Net architecture, the encoders and decoders are designed in such a manner that the network captures finer information and retains more information by concatenating high-level features with low-level ones. This allows the network to yield more accurate results. U-Net Architecture. Source‍ SegNet SegNet is also a deep fully convolutional network that is designed especially for semantic pixel-wise segmentation. Like U-Net, SegNet’s architecture also consists of encoder and decoder blocks. The SegNet differs from other neural networks in the way it uses its decoder for upsampling the features. The decoder network uses the pooling indices computed in the max-pooling layer which in turn makes the encoder perform non-linear upsampling. This eliminates the need for learning to upsample. SegNet is primarily designed for scene-understanding applications. SegNet Architecture. Source DeepLab DeepLab is primarily a convolutional neural network (CNN) architecture. Unlike the other two networks, it uses features from every convolutional block and then concatenates them to their deconvolutional block. The neural network uses the features from the last convolutional block and upsamples it like the fully convolutional network (FCN). It uses the atrous convolution or dilated convolution method for upsampling. The advantage of atrous convolution is that the computation cost is reduced while capturing more information. The encoder-Decoder architecture of DeepLab v3. Source Foundation Model Techniques Foundation models have also been used for image segmentation, which divides an image into distinct regions or segments. Unlike language models, which are typically based on transformer architectures, foundation models for image segmentation often use convolutional neural networks (CNNs) designed to handle image data. Segment Anything Model Segment Anything Model (SAM) is considered the first foundation model for image segmentation. SAM is built on the largest segmentation dataset to date, with over 1 billion segmentation masks. It is trained to return a valid segmentation mask for any prompt, where a prompt can be foreground/background points, a rough box or mask, freeform text, or general information indicating what to segment in an image. Under the hood, an image encoder produces a one-time embedding for the image, while a lightweight encoder converts any prompt into an embedding vector in real time. These two information sources are combined in a lightweight decoder that predicts segmentation masks.‍ Source Metrics for Evaluating Image Segmentation Algorithms Pixel Accuracy Pixel accuracy is a common evaluation metric used in image segmentation to measure the overall accuracy of the segmentation algorithm. It is defined as the ratio of the number of correctly classified pixels to the total number of pixels in the image. Pixel accuracy is a straightforward and easy-to-understand metric that provides a quick assessment of the segmentation performance. However, it does not account for the spatial alignment between the ground truth and the predicted segmentation, which can be important in some applications. In addition, pixel accuracy can be sensitive to class imbalance, where one class has significantly more pixels than another. This can lead to a biased evaluation of the algorithm's performance. Dice Coefficient The dice coefficient measures the similarity between two sets of binary data, in this case, the ground truth segmentation and the predicted segmentation. The dice coefficient is calculated as Where intersection is the number of pixels that are correctly classified as positive by both the ground truth and predicted segmentations, and ground truth and predicted are the total number of positive pixels in the respective segmentations. The Dice coefficient ranges from 0 to 1, with higher values indicating better segmentation performance. A value of 1 indicates a perfect overlap between the ground truth and predicted segmentations. The Dice coefficient is a popular metric for image segmentation because it is sensitive to small changes in the segmentation and is not affected by class imbalance. However, it does not account for the spatial alignment between the ground truth and predicted segmentation, which can be important in some applications. Jaccard Index (IOU) The Jaccard index, also known as the intersection over union (IoU) score, measures the similarity between the ground truth segmentation and the predicted segmentation. It is formulated as Where intersection is the number of pixels that are correctly classified as positive by both the ground truth and predicted segmentations, and ground truth and predicted are the total number of positive pixels in the respective segmentations. The IoU score ranges from 0 to 1, with higher values indicating better segmentation performance. A value of 1 indicates a perfect overlap between the ground truth and predicted segmentations. The Jaccard index takes into account both the true positives and false positives and is not affected by class imbalance. It also accounts for the spatial alignment between the ground truth and predicted segmentations. Datasets for Evaluating Image Segmentation Algorithms The evaluation of image segmentation algorithms is a crucial task n computer vision research. To measure the performance of these algorithms, various benchmark datasets have been developed. We will be discussing three popular datasets for evaluating image segmentation algorithms. These datasets provide carefully annotated images with pixel-level annotations, allowing researchers to test and compare the effectiveness of their segmentation algorithms. Barkley Segmentation Dataset and Benchmark The Barkley Segmentation Dataset is a standard benchmark for contour detection. This dataset is intended for testing natural edge detection, which takes into account background boundaries in addition to object interior and exterior boundaries as well as object contours. It includes 500 natural images with carefully annotated boundaries collected from multiple users. The dataset is divided into three parts: 200 for training, 100 for validation, and the rest 200 for testing. Pascal VOC Segmentation Dataset The Pascal VOC Segmentation Dataset is a popular benchmark dataset for evaluating image segmentation algorithms. It contains images from 20 object categories and provides pixel-level annotations for each image. The dataset is divided into the train, validation, and test sets, with the test set used to evaluate the performance of segmentation algorithms. The Pascal VOC Segmentation Dataset has been used as a benchmark for various computer vision challenges, including the Pascal VOC Challenge and the COCO Challenge. MS COCO Segmentation Dataset The Microsoft Common Objects in Context (COCO) Segmentation Dataset is another widely used dataset for evaluating image segmentation algorithms. It contains over 330,000 images with object annotations, including segmentations of 80 object categories. The dataset is divided into the train, validation, and test sets, with the test set containing around 5,000 images. The MS COCO Segmentation Dataset is often used as a benchmark for evaluating segmentation algorithms in various computer vision challenges, including the COCO Challenge. Future Direction of Image Segmentation Auto-Segmentation with SAM Auto-segmentation refers to the process of automatically segmenting an image without human intervention. Auto-segmentation with Meta’s Segment Anything Model (SAM) has instantly become popular as it shows remarkable performance in image segmentation tasks. It is a single model that can easily perform both interactive segmentation and automatic segmentation. Since SAM is trained on a diverse, high-quality dataset, it can generalize to new types of objects and images beyond what is observed during training. This ability to generalize means that by and large, practitioners will no longer need to collect their segmentation data and fine-tune a model for their use case. Improvement in segmentation accuracy Improving segmentation accuracy is one of the main goals of researchers in the field of computer vision. Accurate segmentation is essential for various applications, including medical imaging, object recognition, and autonomous vehicles. While deep learning techniques have led to significant improvements in segmentation accuracy in recent years, there is still much room for improvement. Here are some ways researchers are working to improve segmentation accuracy: Incorporating additional data sources: One approach to improving segmentation accuracy is incorporating additional data sources beyond the raw image data. For example, depth information can provide valuable cues for object boundaries and segmentation, particularly in complex scenes with occlusions and clutter. Developing new segmentation algorithms: Researchers continuously develop new algorithms for image segmentation that can improve accuracy. For example, some recent approaches use adversarial training or reinforcement learning to refine segmentation results. Improving annotation quality: The quality of the ground truth annotations used to train segmentation algorithms is essential to achieving high accuracy. Researchers are working to improve annotation quality through various means, including incorporating expert knowledge and utilizing crowdsourcing platforms. Refining evaluation metrics: Evaluation metrics play a crucial role in measuring the accuracy of segmentation algorithms. Researchers are exploring new evaluation metrics beyond the traditional Dice coefficient and Jaccard index, such as the Boundary F1 score, which can better capture the quality of object boundaries. Integrate Deep Learning with Traditional Techniques While deep learning techniques have shown remarkable performance in segmentation tasks, traditional techniques such as clustering, thresholding, and morphological operations can still provide useful insights and improve accuracy. Here are some ways researchers are integrating deep learning with traditional techniques in image segmentation: Hybrid models: Researchers are developing hybrid models that combine deep learning with traditional techniques. For example, some approaches use clustering or thresholding to initialize deep learning models or post-process segmentation results. Multi-stage approaches: Multi-stage approaches involve using deep learning for initial segmentation and then refining the results using traditional techniques. For example, some approaches use morphological operations to smooth and refine segmentation results. Attention-based models: Attention-based models are a type of deep learning model that incorporates traditional techniques for computing attention weights within a feature map. Attention-based models can improve accuracy by focusing on relevant image features and ignoring irrelevant ones. Transfer learning: Transfer learning involves pretraining deep learning models on large datasets and then fine-tuning them for specific segmentation tasks. Traditional techniques such as clustering or thresholding can be used to identify relevant features for transfer learning. Applications of Image Segmentation Image segmentation has a wide range of applications in various fields, including medical imaging, robotics, autonomous vehicles, and surveillance. Here are some examples of how image segmentation is used in different fields: Medical imaging: Image segmentation is widely used in medical imaging for tasks such as tumor detection, organ segmentation, and disease diagnosis. Accurate segmentation is essential for treatment planning and monitoring disease progression. Robotics: Image segmentation is used in robotics for object recognition and manipulation. For example, robots can use segmentation to recognize and grasp specific objects, such as tools or parts, in industrial settings. Autonomous vehicles: Image segmentation is essential for the development of autonomous vehicles, allowing them to detect and classify objects in their environment, such as other vehicles, pedestrians, and obstacles. Accurate segmentation is crucial for safe and reliable autonomous navigation. Surveillance: Image segmentation is used in surveillance for detecting and tracking objects and people in real-time video streams. Segmentation can help to identify and classify objects of interest, such as suspicious behavior or potential threats. Agriculture: Image segmentation is used in agriculture for crop monitoring, disease detection, and yield prediction. Accurate segmentation can help farmers make informed decisions about crop management and optimize crop yields. Art and design: Image segmentation is used in art and design for tasks such as image manipulation, color correction, and style transfer. Segmentation can help to separate objects or regions of an image and apply different effects or modifications to them. Image Segmentation: Key Takeaways Image segmentation is a powerful technique that allows us to identify and separate different objects or regions within an image. It has a wide range of applications in fields such as medical imaging, robotics, and computer vision. In this guide, we covered various image segmentation techniques, including traditional techniques such as thresholding, region-based segmentation, edge-based segmentation, and clustering, as well as deep learning and foundation model techniques. We also discussed different evaluation metrics and datasets used to evaluate segmentation algorithms. As image segmentation continues to advance, future directions will focus on improving segmentation accuracy, integrating deep learning with traditional techniques, and exploring new applications in various fields. Auto-segmentation with the Segment Anything Model (SAM) is a promising direction that can reduce manual intervention and improve accuracy. Integration of deep learning with traditional techniques can also help to overcome the limitations of individual techniques and improve overall performance. With ongoing research and development, we can expect image segmentation to continue to make significant contributions to various fields and industries. Further Reading on Image Segmentation Comparing Two Object Segmentation Models: Mask-RCNN vs. Personalized-SAM Deep Learning Techniques for Medical Image Segmentation: Achievements and Challenges Visual Segmentation of “Simple” Objects for Robots Best practices in deep learning based segmentation of microscopy image Image segmentation: Papers with code

Nov 07 2022

15 M

Software To Help You Turn Your Data Into AI

Forget fragmented workflows, annotation tools, and Notebooks for building AI applications. Encord Data Engine accelerates every step of taking your model into production.