Confusion Matrix

A confusion matrix is a performance evaluation tool used in machine learning that summarizes the performance of a classification model by tabulating true positive, true negative, false positive, and false negative predictions. It helps assess the accuracy and effectiveness of the model's predictions.The matrix is based on the concepts of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN). It provides a granular view of a model's performance across different classes.

Let's take a closer look at the components of a confusion matrix and how they can help evaluate a model's predictive power.

Structure

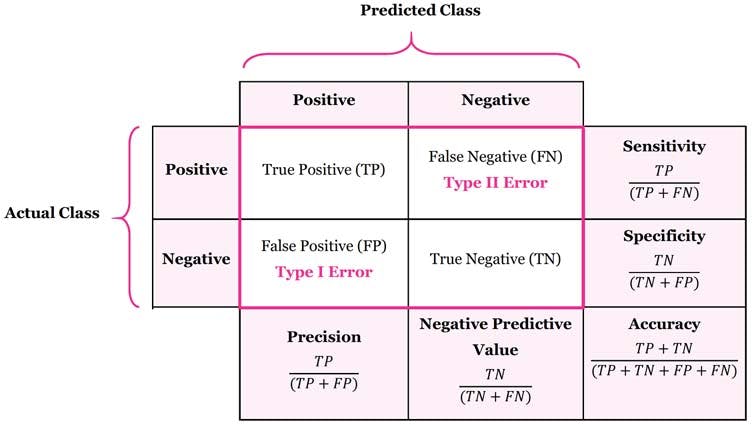
• True Positives (TP): Instances where the model correctly predicts a positive class when it is indeed positive. Consider a cancer diagnostic model: a true positive would occur when the model correctly identifies a patient with cancer as having the disease. TP is a vital measure of the model's ability to recognize positive instances accurately.
• True Negatives (TN): Instances where the model correctly predicts a negative class when it is indeed negative. Continuing the medical analogy, a true negative would be when the model correctly identifies a healthy patient as not having the disease. TN reflects the model's proficiency in recognizing negative instances.
• False Positives (FP): Instances where the model incorrectly predicts a positive class when it should have been negative. In the medical scenario, a false positive would mean the model wrongly indicates a patient has the disease when they are, in fact, healthy. FP illustrates instances where the model exhibits overconfidence in predicting positive outcomes.
• False Negatives (FN): Instances where the model incorrectly predicts a negative class when it should have been positive. In the medical context, a false negative would be when the model fails to detect a disease in a patient who actually has it. FN highlights situations where the model fails to capture actual positive instances.

Confusion Matrix

The confusion matrix serves as the basis for calculating essential evaluation metrics that offer nuanced insights into a model's performance:

• Accuracy: Accuracy quantifies the ratio of correct predictions (TP and TN) to the total number of predictions. While informative, this metric can be misleading when classes are imbalanced.
• Precision: Precision evaluates the proportion of true positive predictions among all positive predictions (TP / (TP + FP)). This metric is crucial when the cost of false positives is high. 
• Recall (Sensitivity or True Positive Rate): Recall measures the ratio of true positive predictions to the actual number of positive instances (TP / (TP + FN)). This metric is significant when missing positive instances is costly.
• Specificity (True Negative Rate): Specificity calculates the ratio of true negative predictions to the actual number of negative instances (TN / (TN + FP)). This metric is vital when the emphasis is on accurately identifying negative instances.
• F1-Score: The F1-Score strikes a balance between precision and recall, making it useful when both false positives and false negatives carry similar importance.

Applications of the Confusion Matrix

The confusion matrix has applications across various fields:

• Model Evaluation: The primary application of the confusion matrix is to evaluate the performance of a classification model. It provides insights into the model's accuracy, precision, recall, and F1-score.
• Medical Diagnosis: The confusion matrix finds extensive use in medical fields for diagnosing diseases based on tests or images. It aids in quantifying the accuracy of diagnostic tests and identifying the balance between false positives and false negatives. 
• Fraud Detection: Banks and financial institutions use confusion matrices to detect fraudulent transactions by showcasing how AI algorithms help identify patterns of fraudulent activities.
• Natural Language Processing (NLP): NLP models use confusion matrices to evaluate sentiment analysis, text classification, and named entity recognition. 
• Customer Churn Prediction: Confusion matrices play a pivotal role in predicting customer churn and show how AI-driven models use historical data to anticipate and mitigate customer attrition.
• Image and Object Recognition: Confusion matrices assist in training models to identify objects in images, enabling technologies like self-driving cars and facial recognition systems.
• A/B Testing: A/B testing is crucial for optimizing user experiences. Confusion matrices help analyze the results of A/B tests, enabling data-driven decisions in user engagement strategies.