Triplet Loss

Triplet Loss is a specialized loss function designed to encourage embeddings of similar data points to converge closer together within the feature space, while simultaneously pushing embeddings of dissimilar data points to drift further apart. The term "triplet" refers to a trio of data points: an anchor point, a positive point, and a negative point. The anchor point is the central data point for which an embedding is to be learned, the positive point is a data point similar to the anchor (e.g., an image of the same individual), and the negative point is a data point that is starkly different from the anchor (e.g., an image of an unrelated individual).

Mathematically, Triplet Loss can be expressed as:

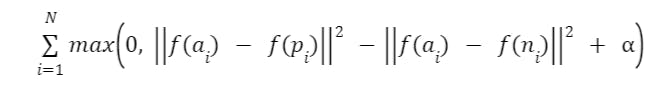
Where:

• f() symbolizes the function responsible for generating embeddings.
• a = anchor image
• p denotes positive image
• n denote the negative image
• Ɑ represents a margin hyperparameter setting a lower limit on the separation between the distances of positive and negative embeddings.

The core of the triplet loss function lies in the margin α, a hyperparameter that set the minimum difference required between the squared distances of anchor-positive and anchor-negative embeddings. By imposing this margin, the loss function encourages a desirable spread between positive and negative distances, creating an environment conducive to learning meaningful representations. These positive and negative distances are calculated using distance metric, usually euclidean distance. 

The foundation of Triplet Loss is the fundamental goal of learning embeddings that highlight the inherent relationships between data points. This is distinct from conventional loss functions, which are primarily designed for tasks like categorization or value prediction. In scenarios such as face recognition, where the nuances of facial features are crucial, embeddings (or encodings) that can differentiate between individuals in a way that is not easily achievable by raw pixels are invaluable.

Triplet Loss emerges as a solution to this challenge. By encouraging the neural network to learn embeddings based on the context of positive and negative instances relative to anchor instances, opens the gateway to the acquisition of discriminating features that inherently capture the essence of the data relationships.

Triplet Loss made its debut in 2015 within the framework of FaceNet: A Unified Embedding for Face Recognition and Clustering. Since then, it has gained widespread recognition as a go-to loss function for tasks involving supervised similarity or metric learning.

 

Triplet Selection Strategies

Selecting appropriate triplets is crucial for the effectiveness of Triplet Loss. In practice, randomly selecting triplets may lead to slow convergence or suboptimal solutions. Therefore, several strategies are employed to efficiently choose informative triplets:

• Online Triplet Mining: Instead of using all possible triplets, online triplet mining selects triplets based on their loss value. Only the most challenging triplets, i.e., those with loss values close to zero, are used for gradient computation. This approach accelerates convergence and focuses the learning process on difficult examples.

• Hard Negative Mining: The negative sample chosen for a triplet should be harder to distinguish from the anchor than the positive sample. Hard negative mining involves selecting the negative sample that violates the margin most, thereby ensuring that the network learns more effectively from challenging instances.

• Semi-Hard Negative Mining: It aims to strike a balance between randomly selected negatives and hard negatives. Semi-hard negatives are negatives that are farther from the anchor than the positive but still have a positive loss value. They provide a middle ground, helping the network generalize better without converging to a trivial solution.

Variations of Triplet Loss

The basic formulation of Triplet Loss has led to several variations and enhancements to improve its effectiveness:

• Batch Hard Triplet Loss: Instead of selecting the hardest negative for each anchor-positive pair, this method considers the hardest negative within a batch of training examples. This accounts for intra-batch variations and can be computationally efficient.

• Contrastive Loss: Triplet Loss can be seen as an extension of Contrastive Loss, where instead of triplets, pairs of anchor-positive and anchor-negative examples are considered.

• Quadruplet Loss: This extension involves adding a second positive example to the triplet, further emphasizing the relationship between the anchor and the positive instances.

• Proxy-based Losses: Proxy-based methods involve learning a set of proxy vectors that represent different classes. These proxies serve as landmarks in the embedding space, making it easier to form triplets and learn meaningful representations.

Applications of Triplet Loss

Triplet Loss has applications in various domains, particularly in cases where learning meaningful embeddings is essential:

• Face Recognition: One of the earliest applications of Triplet Loss was in the field of computer vision, specifically face recognition. By learning embeddings that minimize intra-personal variations and maximize inter-personal differences, Triplet Loss helps create robust and discriminative facial embeddings.

• Image Retrieval: Triplet Loss can be used to build content-based image retrieval systems. Images are encoded into embeddings, and retrieving similar images becomes a matter of finding embeddings that are close to the query image's embedding.

• Person Re-identification: In scenarios like video surveillance, Triplet Loss can be used to develop models that recognize the same person across different camera views, even under varying lighting and poses.

• Information Retrieval: In natural language processing, Triplet Loss can be adapted to learn embeddings for text documents, enabling similarity-based search and clustering.

The implementation of triplet loss can be found in popular machine learning frameworks such as PyTorch and TensorFlow, where dedicated loss functions are available.

Triplet Loss: Challenges

While Triplet Loss presents a compelling solution for machine learning algorithms aiming to learn meaningful embeddings, it is not without its challenges:

• Data Imbalance: The distribution of positive and negative pairs can be imbalanced, leading to the network focusing more on the abundant class. Addressing this requires careful triplet selection or balancing mechanisms.

• Margin Tuning: The choice of margin (α) affects the convergence and stability of the training process. It might require manual tuning or experimentation to find an optimal value.

• Computational Demands: Computationally, training with triplet loss can be demanding, especially when dealing with large datasets. Batch strategies and hardware optimization become essential.

Triplet Loss: Key Takeaways

• Data Relationships: Triplet Loss highlights data relationships, benefiting tasks like face recognition and image retrieval.

• Triplets Defined: Triplet Loss operates on anchor, positive, and negative data points to minimize anchor-positive distance and maximize anchor-negative distance.

• Margin Significance: The margin parameter (α) enforces a minimum separation between positive and negative distance, shaping the embedding space.

• Applications and Challenges: Triplet Loss is used in face recognition, retrieval, etc. Challenges include data imbalance, margin tuning, and computational demands. Strategies like online triplet mining and variations help mitigate challenges.