Introduction to Krippendorff's Alpha: Inter-Annotator Data Reliability Metric in ML

Krippendorff's Alpha is a statistical measure developed to quantify the agreement among different observers, coders, judges, raters, or measuring instruments when assessing a set of objects, units of analysis, or items. 

For example, imagine a scenario where several film critics rate a list of movies. If most critics give similar ratings to each movie, there's high agreement, which Krippendorff's Alpha can quantify. This agreement among observers is crucial as it helps determine the reliability of the assessments made on the films. 

This coefficient emerged from content analysis but has broad applicability in various fields where multiple data-generating methods are applied to the same entities. The key question Krippendorff's Alpha helps answer is how much the generated data can be trusted to reflect the objects or phenomena studied.

What sets Krippendorff's Alpha apart is its ability to adapt to various data types—from binary to ordinal and interval-ratio—and handle multiple annotator categories, providing a nuanced analysis where other measures like Fleiss' kappa might not suffice. Particularly effective in scenarios with more than two annotators or complex ordinal data, it is also robust against missing data, ignoring such instances to maintain accuracy.

This blog aims to demystify Krippendorff's Alpha, offering a technical yet accessible guide. We'll explore its advantages and practical applications, empowering you to enhance the credibility and accuracy of your data-driven research or decisions.

Mathematical Foundations of Krippendorff's Alpha

Krippendorff's Alpha is particularly useful because it can accommodate different data types, including nominal, ordinal, interval, and ratio, and can be applied even when incomplete data. This flexibility makes it a robust choice for inter-rater reliability assessments compared to other methods like Fleiss' kappa.

Definition and Formula

Krippendorff's Alpha, α, defined as 1 - the ratio of observed and expected disagreement.

Krippendorff's Alpha Equation

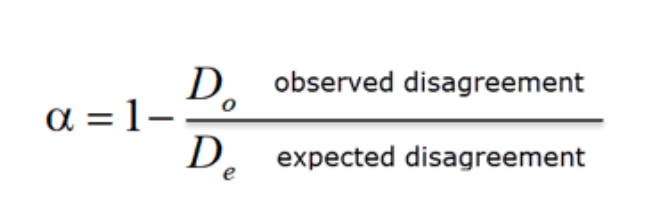
• Observed Agreement (Do): This measures the actual agreement observed among the raters. It's calculated using a coincidence matrix that cross-tabulates the data's pairable values.
• Chance Agreement (De): This represents the amount of agreement one might expect to happen by chance. It's an essential part of the formula as it adjusts the agreement score by accounting for the probability of random agreement.
• Disagreement: In the context of Krippendorff's Alpha, disagreement is quantified by calculating both observed and expected disagreements (Do and De).

Applying Krippendorff's Alpha

To calculate Krippendorff's Alpha:

1. Prepare the data: Clean and organize the dataset, eliminating units with incomplete data if necessary.
2. Build the agreement table: Construct a table that shows how often each unit received each rating to form the basis for observed agreement calculations.
3. Calculate Observed Agreement (Do): It involves detailed calculations considering the distribution of ratings and the frequency of each rating per unit. Specifically, for each pair of ratings, you assess whether they agree or disagree, applying an appropriate weight based on the measurement level (nominal, ordinal, etc.).
4. Calculate Expected Agreement by Chance (De): Calculate the classification probability for each rating category. You then sum the products of these probabilities, accounting for the chance that raters might agree randomly.
5. Determine Krippendorff's Alpha: Finally, calculate Alpha using the revised formula:
   
   The formula represents a variation of Krippendorff's Alpha. This variation of the Alpha coefficient is particularly useful when dealing with more straightforward cases of agreement. It normalizes the agreement relative to chance, providing a more robust understanding of the inter-rater reliability than a simple percentage agreement.

Interpreting Krippendorff's Alpha

Krippendorff's Alpha values range from -1 to +1, where:

• +1 indicates perfect reliability.
• 0 suggests no reliability beyond chance.
• An alpha less than 0 implies systematic disagreements among raters

Due to its ability to handle different data types and incomplete data sets, Krippendorff's Alpha is a valuable tool in research and data analysis. However, its computation can be more complex than other metrics like Cohen's kappa. If you prefer a more automated approach, tools like the K-Alpha Calculator provide a user-friendly online interface for calculating Krippendorff's Alpha, accommodating various data types and suitable for researchers from diverse fields.

Properties and Assumptions of Krippendorff's Alpha

Krippendorff's Alpha is known for its nonparametric nature, making it applicable to different levels of measurement, such as nominal, ordinal, interval, or ratio data. This flexibility is a significant advantage over other reliability measures that might be restricted to a specific data type. The Alpha coefficient can accommodate any number of units and coders, and it effectively manages missing data, which is often a challenge in real-world research scenarios.

For Krippendorff's Alpha to be applied effectively, certain assumptions need to be met:

Nominal Data and Random Coding

While Krippendorff's Alpha is versatile enough to handle different types of data, it's essential to correctly identify the nature of the data (nominal, ordinal, etc.) to apply the appropriate calculations. For nominal data, disagreements among coders are either complete or absent, while the extent of disagreement can vary for other data types. For example, consider a scenario where coders classify animals like 'Mammals,' 'Birds,' and 'Reptiles.' Here, the data is nominal since these categories do not have a logical order.

Example: Suppose three coders are classifying a set of animals. They must label each animal as 'Mammal,' 'Bird,' or 'Reptile.' Let's say they all classify 'Dog' as a 'Mammal,' which is an agreement. However, if one coder classifies 'Crocodile' as a 'Reptile' and another as a 'Bird,' this is a complete disagreement. No partial agreements exist in nominal data since the categories are distinct and non-overlapping.

In this context, Krippendorff's Alpha will assess the extent of agreement or disagreement among the coders. It is crucial to use the correct level of measurement for the data because it influences the calculation of expected agreement by chance (D_e). For nominal data, the calculation assumes that any agreement is either full or none, reflecting the binary nature of the agreement in this data type.

Limitations and Potential Biases

Despite its advantages, Krippendorff's Alpha has limitations. The complexity of its calculations can be a drawback, especially in datasets with many categories or coders. Moreover, the measure might yield lower reliability scores if the data is heavily skewed towards a particular category or if a high level of agreement is expected by chance.

Regarding potential biases, the interpretation of Krippendorff's Alpha should be contextualized within the specifics of the study. For example, a high Alpha does not necessarily imply absolute data accuracy but indicates a high level of agreement among coders. Researchers must be cautious and understand that agreement does not equate to correctness or truth.

To address these complexities and enhance the application of Krippendorff's Alpha in research, tools like the R package 'krippendorff's alpha' provide a user-friendly interface for calculating the Alpha coefficient. This package supports various data types and offers functionality like bootstrap inference, which aids in understanding the statistical significance of the Alpha coefficient obtained.

While Krippendorff's Alpha is a powerful tool for assessing inter-rater reliability, researchers must be mindful of its assumptions, limitations, and the context of their data to make informed conclusions about the reliability of their findings​​​​.

Statistical Significance and Confidence Intervals

In the context of Krippendorff's Alpha, statistical significance testing and confidence intervals are essential for accurately interpreting the reliability of the agreement measure. Here's an overview of how these concepts apply to Krippendorff's Alpha:

Statistical Significance Testing for Alpha

Statistical significance in the context of Krippendorff's Alpha relates to the likelihood that the observed agreement among raters occurred by chance. In other words, it helps determine whether the measured agreement is statistically significant or simply a result of random chance. This is crucial for establishing the reliability of the data coded by different observers or raters.

Calculating Confidence Intervals for Alpha Estimates

Confidence intervals are a key statistical tool for assessing the reliability of Alpha estimates. They provide a range of values within which the true Alpha value is likely to fall, with a certain confidence level (usually 95%). This range helps in understanding the precision of the Alpha estimate. Calculating these intervals can be complex, especially with smaller or heterogeneous datasets. The R package 'krippendorffsalpha,' can help you calculate these intervals using bootstrap methods to simulate the sampling process and estimate the variability of Alpha.

Importance of statistical testing in interpreting Alpha values

Statistical testing is vital for interpreting Alpha values, offering a more nuanced understanding of the agreement measure. A high Alpha value with a narrow confidence interval can indicate a high level of agreement among raters that is unlikely due to chance. Conversely, a wide confidence interval might suggest that the Alpha estimate is less precise, potentially due to data variability and sample size limitations.

Recent advancements have proposed various estimators and interval estimation methods to refine the understanding of Alpha, especially in complex datasets. These improvements underscore the need for careful selection of statistical methods based on the data.

Applications of Krippendorff's Alpha in Deep Learning and Computer Vision

Krippendorff's Alpha plays a significant role in deep learning and computer vision, particularly in evaluating the agreement in human-machine annotation.

Role of Human Annotation in Training Deep Learning Models

In computer vision, the quality of annotated data is paramount in modeling the underlying data distribution for a given task. This data annotation is typically a manual process where annotators follow specific guidelines to label images or texts. 

The quality and consistency of these annotations directly impact the performance of the algorithms, such as neural networks used in object detection and recognition tasks. Inaccuracies or inconsistencies in these annotations can significantly affect the algorithm's precision and overall performance.

Measuring Agreement Between Human Annotators and Machine Predictions with Alpha

Krippendorff's Alpha measures the agreement between human annotators and machine predictions. This measurement is crucial because it assesses the consistency and reliability of the annotations that serve as training data for deep learning models. By evaluating inter-annotator agreement and consistency, researchers can better understand how the selection of ground truth impacts the perceived performance of algorithms. It provides a methodological framework to monitor the quality of annotations during the labeling process and assess the trustworthiness of an AI system based on these annotations.

Consider image segmentation, a common task in computer vision involving dividing an image into segments representing different objects. Annotators might vary in how they interpret the boundaries or classifications of these segments. Krippendorff's Alpha can measure the consistency of these annotations, providing insights into the reliability of the dataset. Similarly, in text classification, it can assess how consistently texts are categorized, which is vital for training accurate models.

The Krippendorff's Alpha approach is vital in an era where creating custom datasets for specific tasks is increasingly common, and the need for high-quality, reliable training data is paramount for the success of AI applications.

Monitoring Model Drift and Bias

Krippendorff's Alpha is increasingly recognized as a valuable tool in deep learning and computer vision, particularly for monitoring model drift and bias. Here's an in-depth look at how it applies in these contexts:

The Challenge of Model Drift and Bias in Machine Learning Systems

Model drift occurs in machine learning when the model's performance deteriorates over time due to changes in the underlying data distribution or the relationships between variables. This can happen for various reasons, such as changes in user behavior, the introduction of new user bases, or external factors influencing the system, like economic or social changes. Conversely, bias refers to a model's tendency to make systematically erroneous predictions due to flawed assumptions or prejudices in the training data​​.

Using Alpha to Monitor Changes in Agreement

Krippendorff's Alpha can be an effective tool for monitoring changes in the agreement between human and machine annotations over time. This is crucial for identifying and addressing potential biases in model predictions. For instance, if a machine learning model in a computer vision task is trained on biased data, it may perform poorly across diverse scenarios or demographics. We can assess how closely the machine's annotations or predictions align with human judgments by applying Krippendorff's Alpha. This agreement or discrepancy can reveal biases or shifts in the model's performance, signaling the need for model recalibration or retraining.

Detecting and Mitigating Potential Biases in Model Predictions

In deep learning applications like image segmentation or text classification, regularly measuring the agreement between human annotators and algorithmic outputs using Krippendorff's Alpha helps proactively identify biases. For instance, a lower Alpha score could highlight this bias if the algorithm consistently misclassifies texts from a specific demographic or topic in a text classification task. Similarly, Alpha can reveal if the algorithm systematically misidentifies or overlooks certain image features in image segmentation due to biased training data.

Addressing drift and bias

Data scientists and engineers can take corrective actions by continuously monitoring these agreement levels, such as augmenting the training dataset, altering the model, or even changing the model's architecture to address identified biases. This ongoing monitoring and adjustment helps ensure that machine learning models remain accurate and reliable over time, particularly in dynamic environments where data distributions and user behaviors can change rapidly​​​​.

Krippendorff's Alpha is not just a metric; it's a crucial tool for maintaining the integrity and reliability of machine learning systems. Through its systematic application, researchers and practitioners can ensure that their models continue to perform accurately and fairly, adapting to changes in data and society.

Benchmarking and Evaluating Inter-Annotator Agreement

In fields like computer vision and deep learning, the consistency and quality of data annotations are paramount. Krippendorff's Alpha is critical for benchmarking and evaluating these inter-annotator agreements.

Importance of Benchmarking Inter-Annotator Agreements

When annotating datasets, different annotators can have varying interpretations and judgments, leading to data inconsistencies. Benchmarking inter-annotator agreements helps in assessing the reliability and quality of these annotations. It ensures that the data reflects a consensus understanding and is not biased by the subjective views of individual annotators.

Alpha's Role in Comparing Annotation Protocols and Human Annotators

With its ability to handle different data types and accommodate incomplete data sets, Krippendorff's Alpha is especially suited for this task, offering a reliable statistical measure of agreement involving multiple raters​​.

Examples in Benchmarking Studies for Computer Vision Tasks

An example of using Krippendorff's Alpha in benchmarking studies can be found in assessing data quality in annotations for computer vision applications. In a study involving semantic drone datasets and the Berkeley Deep Drive 100K dataset, images were annotated by professional and crowdsourced annotators for object detection tasks. 

The study aimed to measure inter-annotator agreement and cross-group comparison metrics using Krippendorff’s Alpha. This helped evaluate the relative accuracy of each annotator against the group and identify classes that were more difficult to annotate. Such benchmarking is crucial for developing reliable training datasets for computer vision models, as the quality of annotations directly impacts the model's performance​​.

Assessing Data Quality of Annotations with Krippendorff's Alpha

Krippendorff's Alpha is particularly valuable for assessing the quality of annotations in computer vision. It helps in measuring the accuracy of labels and the correctness of object placement in images. By calculating inter-annotator agreement, Krippendorff's Alpha provides insights into the consistency of data annotations. This consistency is fundamental to training accurate and reliable computer vision models. It also helps identify areas where annotators may need additional guidance, thereby improving the overall quality of the dataset​​.

To illustrate this, consider a project involving image annotation where multiple annotators label objects in street scene photos for a self-driving car algorithm. Krippendorff's Alpha can assess how consistently different annotators identify and label objects like pedestrians, vehicles, and traffic signs. Consistent annotations are crucial for the algorithm to learn accurately from the data. In cases of inconsistency or disagreement, Krippendorff's Alpha can help identify specific images or object categories requiring clearer guidelines or additional training for annotators.

By quantifying inter-annotator agreement, Krippendorff's Alpha plays an indispensable role in benchmarking studies, directly impacting the quality of training datasets and the performance of machine learning models. Its rigorous application ensures that data annotations are reliable, accurate, and representative of diverse perspectives, thereby fostering the development of robust, high-performing AI systems.

Krippendorff's Alpha: What’s Next

Potential Advancements

Adding advanced statistical methods like Bootstrap for confidence intervals and parameter estimation to Krippendorff's Alpha can make the measure more reliable in various research situations. Developing user-friendly computational tools, perhaps akin to Kripp.alpha, is another exciting frontier. These tools aim to democratize access to Krippendorff's Alpha, allowing researchers from various fields to incorporate it seamlessly into their work. The potential for these advancements in complex machine learning model training is particularly promising. As models and data grow in complexity, ensuring the quality of training data through Krippendorff's Alpha becomes increasingly critical.

Research Explorations

Researchers and practitioners are encouraged to explore Krippendorff's Alpha further, particularly in emerging research domains. Its application in fields like educational research (edu), where assessing the reliability of observational data (IRR) or survey responses is critical, can provide new insights. Moreover, disciplines under the ASC (Academic Social Science) umbrella, including sociology and psychology, where Scott's Pi and other agreement measures have traditionally been used, could benefit from the robustness of Krippendorff's Alpha.

By embracing Krippendorff's Alpha in these various fields, the academic and research communities can continue to ensure the credibility and accuracy of their findings, fostering a culture of precision and reliability in data-driven decision-making.

Krippendorff's Alpha: Key Takeaways

A key metric for evaluating inter-annotator reliability is Krippendorff's Alpha, a concept Klaus Krippendorff invented and a cornerstone of content analysis. Unlike Cohen's kappa, which is limited to nominal data and a fixed number of raters, Krippendorff's Alpha provides flexibility in handling various data types, including nominal, ordinal, interval, and ratio. It accommodates any number of raters or coders. Its application extends beyond traditional content analysis to machine learning and inter-coder reliability studies.

In modern applications, particularly machine learning, Krippendorff's Alpha is instrumental in monitoring model drift. Quantifying the agreement among data annotators over time helps identify shifts in data characteristics that could lead to model drift. Machine learning models lose accuracy in this scenario due to evolving data patterns. 

In research settings where sample sizes vary and the reliability of coding data is crucial, Krippendorff's Alpha has become a standard tool, often computed using software like SPSS or SAS. It addresses the observed disagreement among annotators and ensures that the percent agreement is not due to chance. The use of a coincidence matrix in its calculation underscores its methodological rigor.