An Introduction to Cross-Entropy Loss Functions

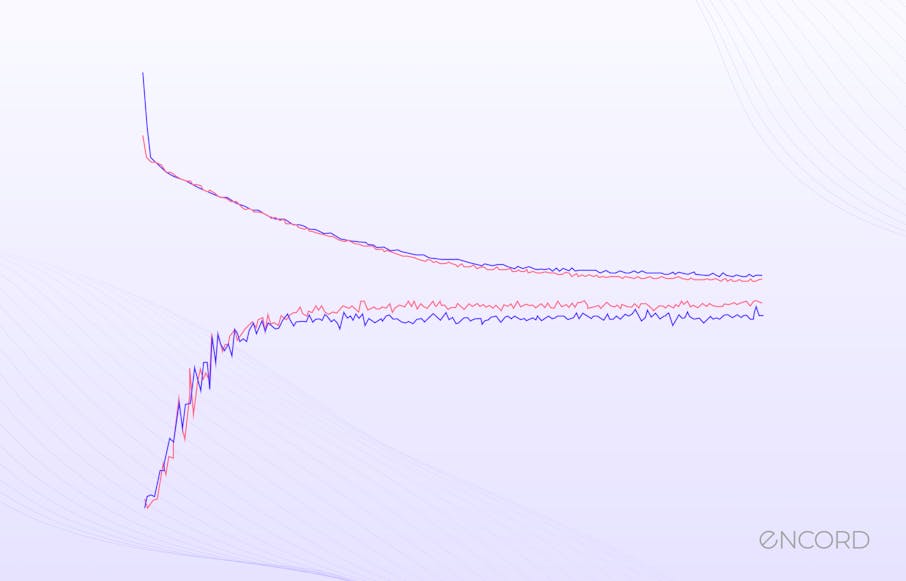
Loss functions are widely used in machine learning tasks for optimizing models. The cross-entropy loss stands out among the many loss functions available, especially in classification tasks. But why is it so significant?

Cross-entropy loss is invaluable in certain scenarios, particularly when interpreting the outputs of neural networks that utilize the softmax function, a common practice in deep learning models. This loss function measures the difference between two probability distributions, reflecting how well the model predicts the actual outcomes.

The term "surrogate loss" refers to an alternative loss function used instead of the actual loss function, which might be difficult to compute or optimize. In this context, cross-entropy can be considered a surrogate for other more complex loss functions, providing a practical approach for model optimization.

In the broader theoretical landscape of machine learning, there's an extensive analysis of a category of loss functions, often referred to in research as "composite loss" or "sum of losses." This category includes cross-entropy (also known as logistic loss), generalized cross-entropy, mean absolute error, and others. These loss functions are integral to providing non-asymptotic guarantees and placing an upper boundary on the estimation error of the actual loss based on the error values derived from the surrogate loss. Such guarantees are crucial as they influence the selection of models or hypotheses during the learning process.

Researchers have been delving into novel loss functions designed for more complex, often adversarial, machine learning environments. For instance, certain innovative loss functions have been crafted by incorporating smoothing terms into traditional forms.

These "smoothed" functions enhance model robustness, especially in adversarial settings where data alterations can mislead learning processes. These advancements are paving the way for new algorithms that can withstand adversarial attacks, fortifying their predictive accuracy.

Foundations of Loss Functions

Loss functions are the backbone of machine learning optimization, serving as critical navigational tools that guide the improvement of models during the training process. These functions present a measure that models strive to minimize, representing the difference or 'loss' between predicted and actual known values. While the concept of maximizing a function, often referred to as a "reward function," exists, particularly in reinforcement learning scenarios, the predominant focus in most machine learning contexts is minimizing the loss function.

Role in Model Optimization

Central to model optimization is the gradient descent process, which adjusts model parameters iteratively to minimize the loss function. This iterative optimization is further powered by backpropagation, an algorithm that calculates the gradient of the loss function concerning the model parameters.

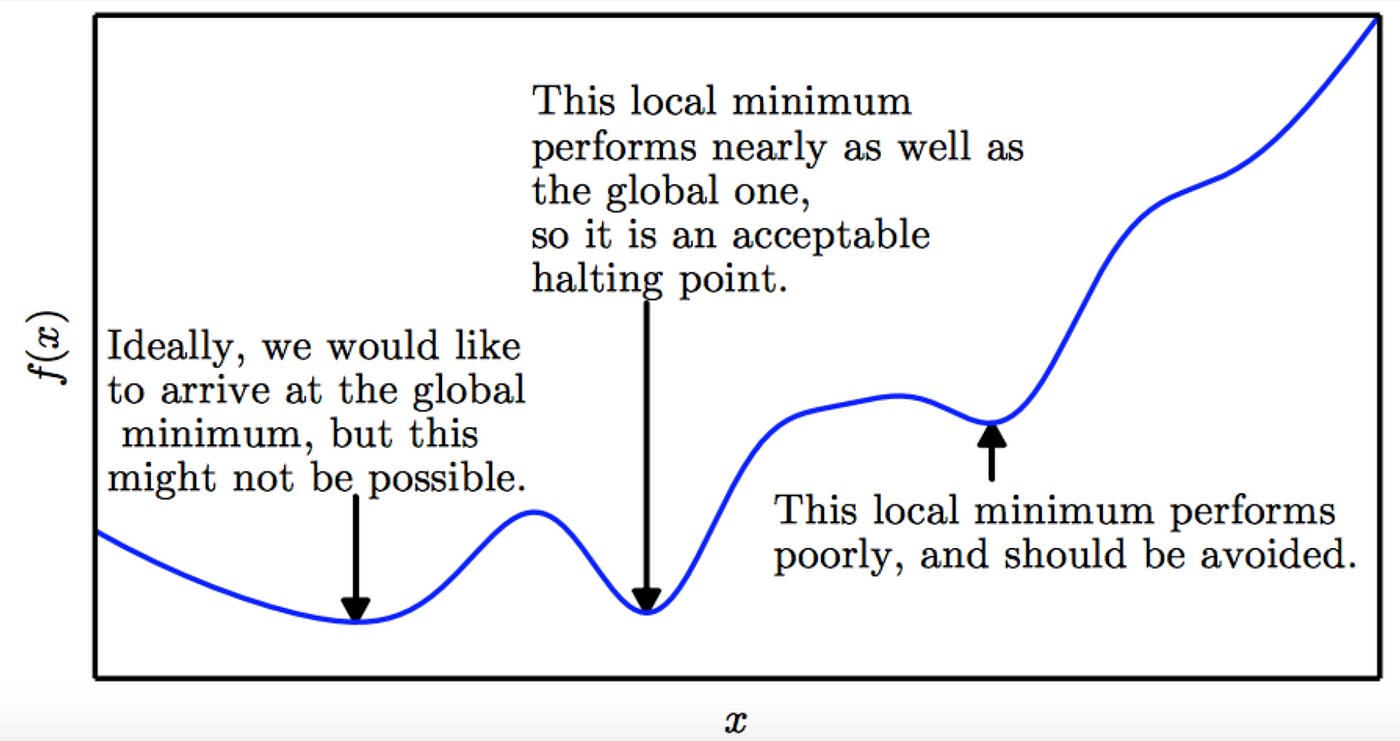
However, the optimization landscape is fraught with challenges. One of the primary concerns is the convergence to local minima instead of the global minimum. In simple terms, while the model might think it has found the optimal solution (local minimum), there might be a better overall solution (global minimum) that remains unexplored.

Explanation of minima/maxima

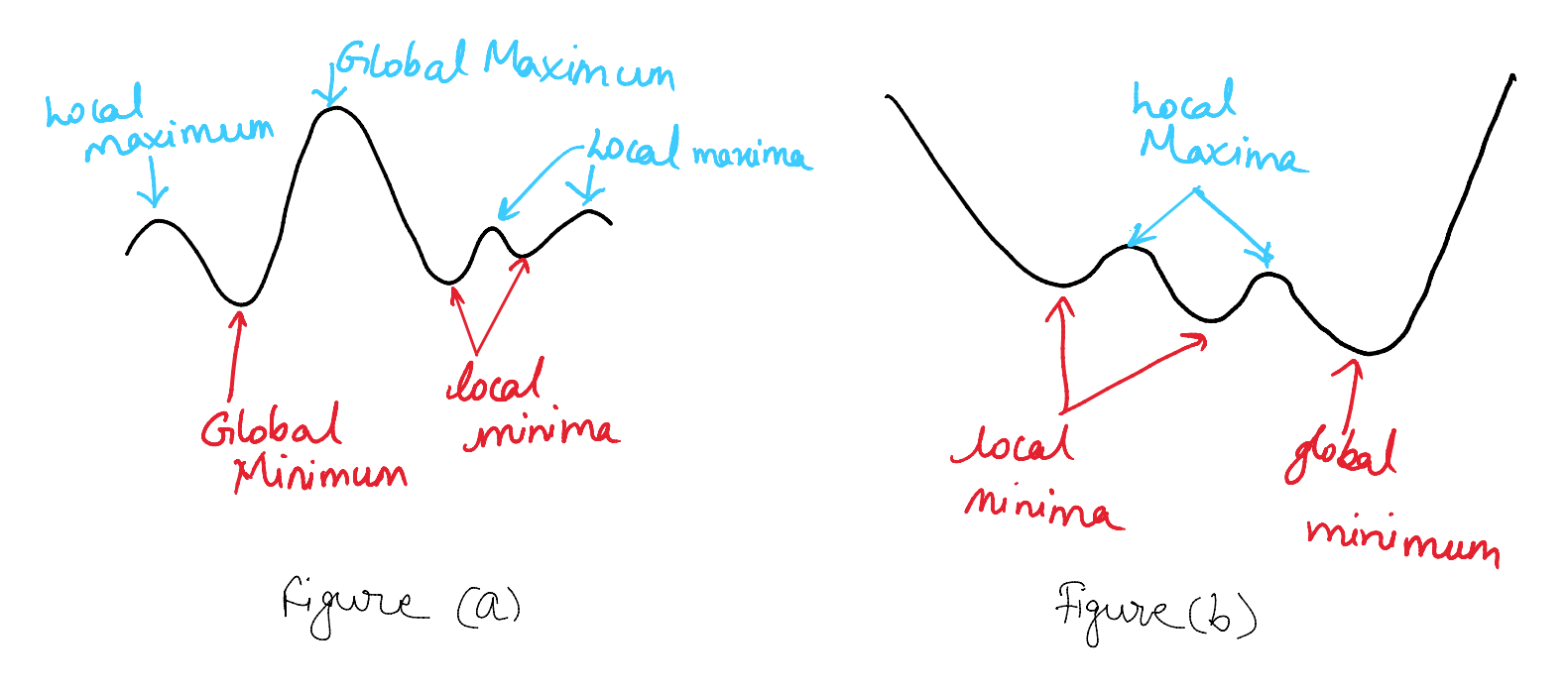
The choice and design of loss functions are crucial for optimal training of ML tasks. For instance, cross-entropy loss, commonly used in classification tasks, has properties such as being convex and providing a clear signal for model updates, making it particularly suitable for such problems. Understanding the nuances of different loss functions, including cross-entropy loss, and their impact on model optimization is essential for developing effective machine learning models.

Common Loss Functions in Machine Learning

Several loss functions have been developed and refined, each tailored to specific use cases.

Mean Squared Error (MSE):

The mean squared error (or MSE) is a quadratic loss function that measures the average squared difference between the estimated values (predictions) and the actual value.

For n samples, it is mathematically represented as 

MSE Loss

MSE Loss is widely used in regression problems. For instance, predicting house prices based on various features like area, number of rooms, and location. A model with a lower MSE indicates a better fit of the model to the data.

Hinge Loss

Hinge loss, or max-margin loss, is used for binary classification tasks. It is defined as

Hinge Loss Function

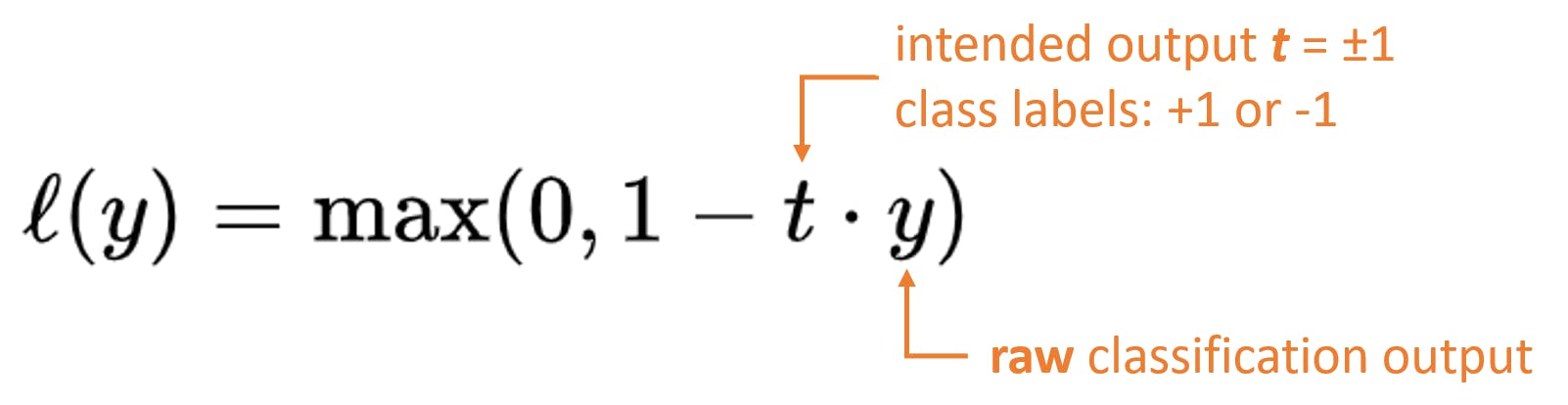
Here, 0 is for correct classifications, and 1 is for wrong classifications.

The hinge loss is near zero if the prediction is correct and with a substantial margin from the decision boundary (high confidence). However, the loss increases as the prediction is either wrong or correct, but with a slim margin from the decision boundary. Hinge loss is commonly associated with Support Vector Machines (SVM). It's used in scenarios where a clear margin of separation between classes is desired, such as in image classification or text categorization.

Log Loss (Logistic Loss)

Log loss quantifies the performance of a classification model where the prediction input is a probability value between 0 and 1. It is defined as:

Log Loss function

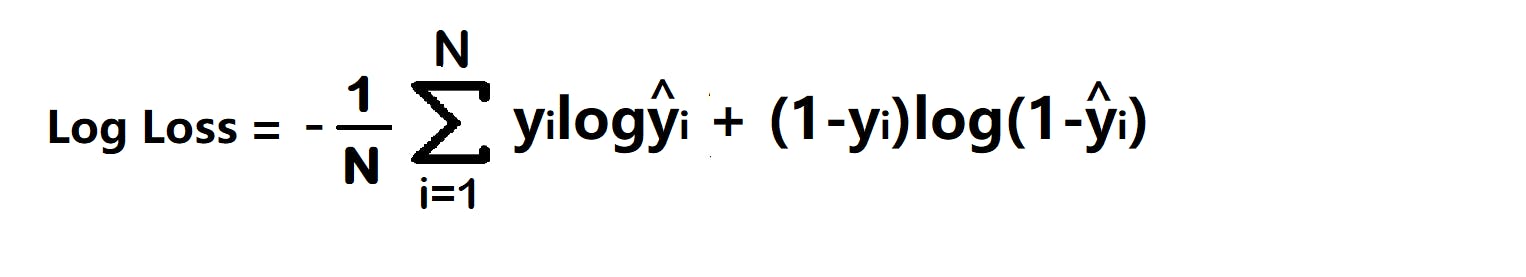
The log loss penalizes both errors (false positives and false negatives), whereas the confidently wrong predictions are more severely penalized.

Log loss is used in logistic regression and neural networks for binary classification problems. It's suitable for scenarios like email spam detection, where you want to assign a probability of an email being spam.

Each loss function has unique characteristics and is chosen based on the problem's nature and the desired output type.

How to select a loss function

Regression: In regression tasks, where the goal is to predict a continuous value, the difference between the predicted and actual values is of primary concern. Common loss functions for regression include:

• Mean Squared Error (MSE): Suitable for problems where large errors are particularly undesirable since they are squared and thus have a disproportionately large impact. The squaring operation amplifies larger errors.
• Mean Absolute Error (MAE): Useful when all errors, regardless of magnitude, are treated uniformly.

Classification: In classification tasks, where the goal is to categorize inputs into classes, the focus is on the discrepancy between the predicted class probabilities and the actual class labels. Common loss functions for classification include:

• Log Loss (Logistic Loss): Used when the model outputs a probability for each class, especially in binary classification.
• Hinge Loss: Used for binary classification tasks, especially with Support Vector Machines, focusing on maximizing the margin.
• Cross-Entropy Loss: An extension of log loss to multi-class classification problems.

The selection of a loss function is not one-size-fits-all. It requires a deep understanding of the problem, the nature of the data, the distribution of the target variable, and the specific goals of the analysis.

Evaluate your models and build active learning pipelines with Encord

Try Encord today

Entropy in Information Theory

Entropy in information theory measures the amount of uncertainty or disorder in a set of probabilities. It quantifies the expected value of the information contained in a message and is foundational for data compression and encryption.

Shannon's Entropy

Shannon's entropy, attributed to Claude Shannon, quantifies the uncertainty in predicting a random variable's value. It is defined as:

Shannon Entropy

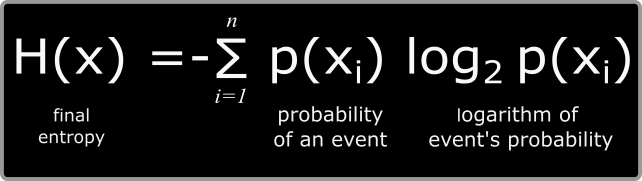
Shannon's entropy is closely related to data compression. It represents the minimum number of bits needed to encode the information contained in a message, which is crucial for lossless data compression algorithms. When the entropy is low (i.e., less uncertainty), fewer bits are required to encode the information, leading to more efficient compression.

Shannon's entropy is foundational for designing efficient telecommunications coding schemes and developing compression algorithms like Huffman coding.

Kullback-Leibler Divergence

Kullback-Leibler (KL) Divergence measures how one probability distribution diverges from a second, expected probability distribution. It is defined as

KL Divergence Equation

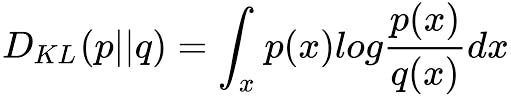
Here are the parameters and their meanings:

• P: The true probability distribution, which serves as the reference.
• Q: The approximate probability distribution is being compared to P.
• x: The event or outcome for which the probabilities are defined.
• P(x): The probability of event x according to the true distribution P.
• Q(x): The probability of event x according to the distribution Q.
• DKL ( p || q ): The KL Divergence quantifies the difference between the two distributions.

KL Divergence is used in model evaluation to measure the difference between predicted probability and true distributions. It is especially useful in scenarios like neural network training, where the goal is to minimize the divergence between the predicted and true distributions.

KL Divergence is often used for model comparison, anomaly detection, and variational inference methods to approximate complex probability distributions.

Cross-Entropy: From Theory to Application

Mathematical Derivation

Cross-entropy is a fundamental concept in information theory that quantifies the difference between two probability distributions. It builds upon the foundational idea of entropy, which measures the uncertainty or randomness of a distribution. The cross-entropy between two distributions, P and Q, is defined as:

Cross Entropy between P & Q

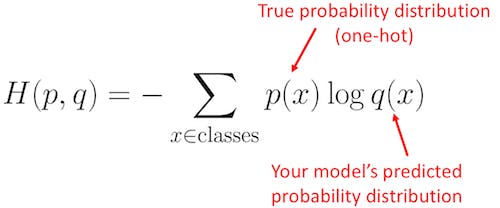
P(x) is the probability of event x in distribution P, and Q(x) is the probability of event x in distribution Q.

1. Log-likelihood function and maximization: The log-likelihood measures how well a statistical model predicts a sample. In machine learning, maximizing the log-likelihood is equivalent to minimizing the cross-entropy between the true data distribution and the model's predictions.

2. Relationship with Kullback-Leibler divergence: The Kullback-Leibler (KL) divergence is another measure of how one probability distribution differs from a second reference distribution.

Cross-entropy can be expressed in terms of KL divergence and the entropy of the true distribution:

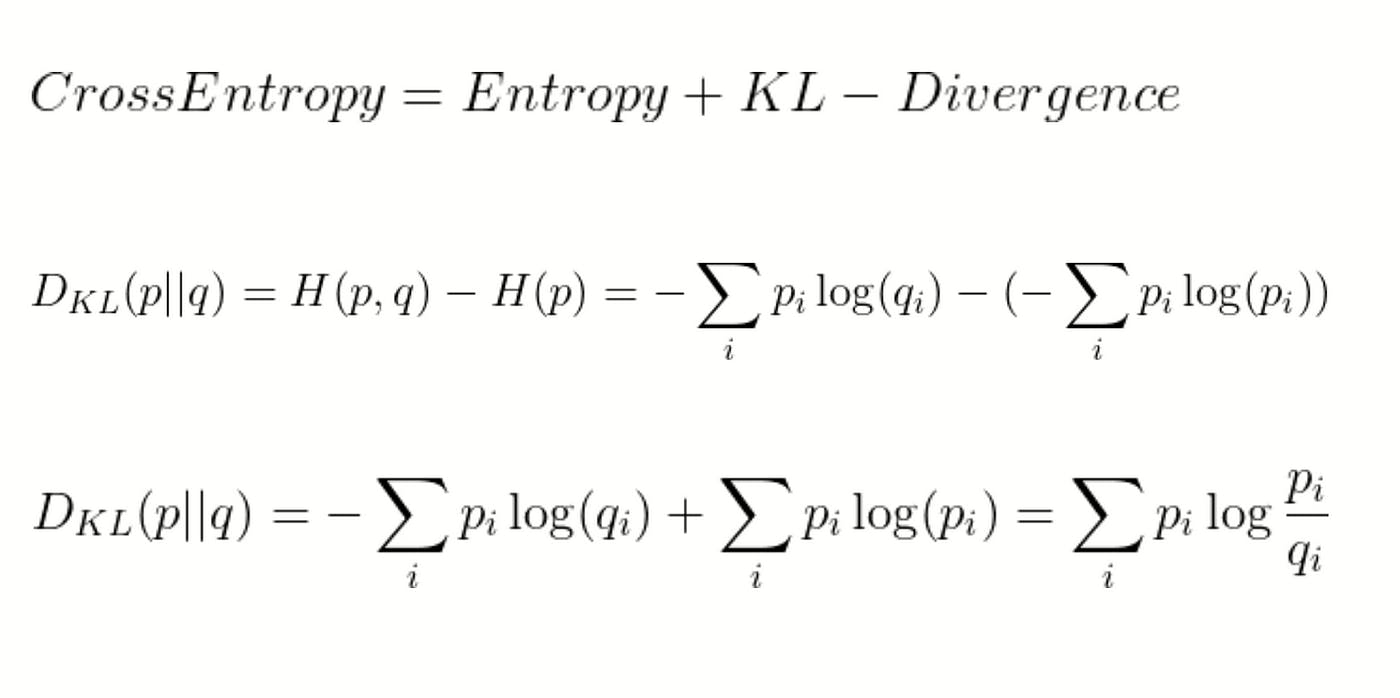
Where H(p) is the entropy of distribution p, and DKL(p || q) is the KL divergence between distributions p and q.

Binary vs. Multi-Class Cross-Entropy

Cross-entropy is a pivotal loss function in classification tasks, measuring the difference between two probability distributions. Cross-entropy formulation varies depending on the nature of the classification task:  binary or multi-class.

Binary Cross-Entropy: This is tailored for binary classification tasks with only two possible outcomes. Given \( y \) as the actual label (either 0 or 1) and \( \hat{y} \) as the predicted probability of the label being 1, the binary cross-entropy loss is articulated as:

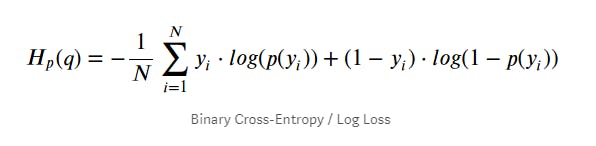
This formulation captures the divergence of the predicted probability from the actual label.

Categorical Cross-Entropy: Suited for multi-class classification tasks, this formulation is slightly more intricate. If \( P \) represents the true distribution over classes and \( Q \) is the predicted distribution, the categorical cross-entropy is given by:

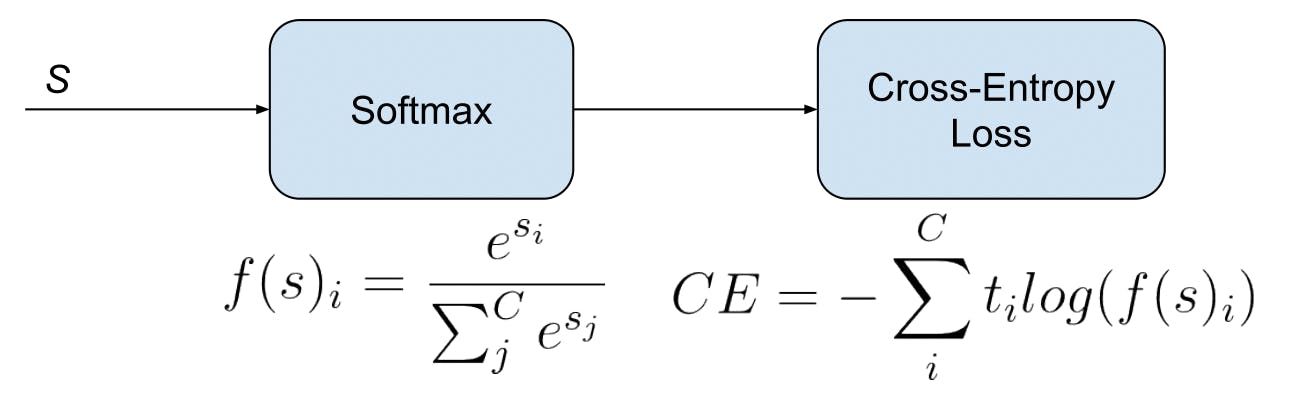
Categorical Cross-Entropy Loss

Here, the loss is computed over all classes, emphasizing the divergence of the predicted class probabilities from the true class distribution.

Challenges in Multi-Class Scenarios: 

The complexity of multi-class cross-entropy escalates with an increase in the number of classes. A fundamental challenge is ensuring that the predicted probabilities across all classes aggregate to one. This normalization is typically achieved using the softmax function, which exponentiates each class score and then normalizes these values to yield a valid probability distribution.

While binary and multi-class cross-entropy aim to measure the divergence between true and predicted distributions, their mathematical underpinnings and associated challenges differ based on the nature of the classification task.

Practical Implications of Cross-Entropy Loss

Cross-entropy loss is pivotal in optimizing models, especially in classification tasks. The implications of cross-entropy loss are vast and varied, impacting the speed of model convergence and regularization (to mitigate overfitting).

Impact on Model Convergence

Speed of Convergence: Cross-entropy loss is preferred in many deep learning tasks because it often leads to faster convergence than other loss functions. It amplifies the gradient when the predicted probability diverges significantly from the actual label, providing a stronger signal for the model to update its weights and thus encouraging faster learning.

Avoiding Local Minima: The nature of the cross-entropy loss function helps models avoid getting stuck in local minima.. Cross-entropy loss penalizes incorrect predictions more heavily than other loss functions, which encourages the model to continue adjusting its parameters significantly until it finds a solution that generalizes well rather than settling for a suboptimal fit.

Local Minima

Regularization and Overfitting

L1 and L2 Regularization: You can combine regularization techniques like L1 (Lasso) and L2 (Ridge) with cross-entropy loss to prevent overfitting.  L1 regularization tends to drive some feature weights to zero, promoting sparsity, while L2 shrinks weights, preventing any single feature from overshadowing others. These techniques add penalty terms to the loss function, discouraging the model from assigning too much importance to any feature.

Dropout and its effect on cross-entropy: Dropout is a regularization technique where random subsets of neurons are turned off during training. This prevents the model from becoming overly reliant on any single neuron. When combined with cross-entropy loss, dropout can help the model generalize better to unseen data.

Implementing Cross-Entropy in Modern Frameworks

PyTorch

In PyTorch, the `nn.CrossEntropyLoss()` function is used to compute the cross-entropy loss. It's important to note that the input to this loss function should be raw scores (logits) and not the output of a softmax function because it combines the softmax activation function and the negative log-likelihood loss in one class. 

import tensorflow as tf

loss_fn = tf.keras.losses.CategoricalCrossentropy()

For binary classification tasks, `tf.keras.losses.BinaryCrossentropy()` is more appropriate:

loss_fn_binary = tf.keras.losses.BinaryCrossentropy()

Custom Loss Functions: TensorFlow and Keras provide flexibility in defining custom loss functions. This can be useful when the standard cross-entropy loss needs to be modified or combined with another loss function for specific applications.

Advanced Topics in Cross-Entropy

Label Smoothing

Label smoothing is a regularization technique that prevents the model from becoming too confident about its predictions. Instead of using hard labels (e.g., [0, 1]), it uses soft labels (e.g., [0.1, 0.9]) to encourage the model to be less certain, distributing certainty between classes.

Improving model generalization: Label smoothing can improve the generalization capability of models by preventing overfitting. Overfitting occurs when a model becomes too confident about its predictions based on the training data, leading to poor performance on unseen data. By using soft labels, label smoothing encourages the model to be less certain, which can lead to better generalization.

Implementation and results: Most deep learning frameworks have label smoothing built-in implementations. For instance, in TensorFlow, it can be achieved by adding a small constant to the true labels and subtracting the same constant from the false labels. The results of using label smoothing can vary depending on the dataset and model architecture. Still, it can generally lead to improved performance, especially in cases where the training data is noisy or imbalanced.

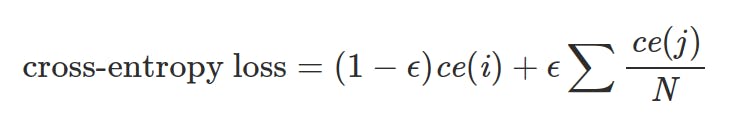
Cross Entropy Loss fn with Label Smoothing

Focal Loss and Class Imbalance

Focal loss is a modification of the standard cross-entropy loss designed to address the class imbalance problem. In datasets with imbalanced classes, the majority class can dominate the loss, leading to poor performance for the minority class.

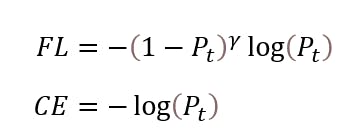
Focal Loss and Cross-Entropy Equation

Origins and Context: The paper "Focal Loss for Dense Object Detection" delves into the challenges faced by one-stage object detectors, which have historically lagged behind the accuracy of two-stage detectors despite their potential for speed and simplicity. The authors identify the extreme foreground-background class imbalance during the training of dense detectors as the primary culprit. The core idea behind Focal Loss is to reshape the standard cross-entropy loss in a way that down-weights the loss assigned to well-classified examples. This ensures that the training focuses more on a sparse set of hard-to-classify examples, preventing the overwhelming influence of easy negatives.

Addressing the class imbalance problem: Focal loss adds a modulating factor to the cross-entropy loss, which down-weights the loss contribution from easy examples (i.e., examples from the majority class) and up-weights the loss contribution from hard examples (i.e., examples from the minority class). This helps the model focus more on the minority class, leading to better performance on imbalanced datasets.

Performance Implications: By focusing more on the minority class, focal loss can lead to improved performance on minority classes without sacrificing performance on the majority class. This makes it a valuable tool for tasks where the minority class is particularly important, such as medical diagnosis or fraud detection.

Focal Loss Formula

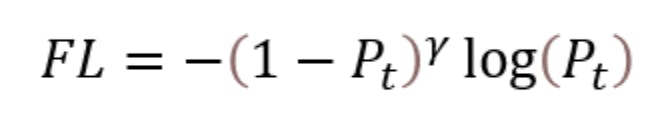
The parameters are:

• p_t is the model's estimated probability for the class with the true label t.
• alpha: A balancing factor, typically between 0 and 1, which can be set differently for each class.
• gamma: A focusing parameter, typically greater than 0, reduces the relative loss for well-classified examples, focusing more on hard, misclassified examples.

Cross Entropy: Key Takeaways

Cross-Entropy Loss as a Performance Measure: Cross-entropy loss is crucial in classification tasks because it quantifies the difference between the predicted probability distribution of the model and the actual distribution of the labels. It is particularly effective when combined with the softmax function in neural networks, providing a clear gradient signal that aids in faster and more efficient model training.

Role of Loss Functions in Optimization: Loss functions like cross-entropy guide the training of machine learning models by providing a metric to minimize. The design of these functions, such as the convexity of cross-entropy, is essential to avoid local minima and ensure that the model finds the best possible parameters for accurate predictions.

Handling Class Imbalance with Focal Loss: Focal loss is an adaptation of cross-entropy that addresses class imbalance by focusing training on hard-to-classify examples. It modifies the standard cross-entropy loss by adding a factor that reduces the contribution of easy-to-classify examples, thus preventing the majority class from overwhelming the learning process.

Regularization Techniques to Prevent Overfitting: Combining cross-entropy loss with regularization techniques like L1 and L2 regularization, or dropout, can prevent overfitting. These methods add penalty terms to the loss function or randomly deactivate neurons during training, encouraging the model to generalize to new, unseen data.

Label Smoothing for Improved Generalization: Label smoothing is a technique that uses soft labels instead of hard labels during training, which prevents the model from becoming overly confident about its predictions. This can lead to better generalization to unseen data by encouraging the model to distribute its certainty among the possible classes rather than focusing too narrowly on the classes observed in the training set.

Evaluate your models and build active learning pipelines with Encord

Try Encord today